Title: The Cheat with the Ace of Clubs
Creator: Georges de La Tour
Creator Lifespan: 1593 - 1652
Creator Nationality: French
Creator Gender: Male
Date Created: c. 1630–34
Physical Dimensions: 38 1/2 x 61 1/2 in. (97.8 x 156.2 cm)
Medium: Oil on canvas
Japanese: French
Century: 17th century
常见问题
损失函数、代价函数、目标函数
首先给出结论:
- 损失函数和代价函数是同一个东西
- 目标函数是一个与他们相关但更广的概念,对于目标函数来说在有约束条件下的最小化就是
损失函数(loss function)
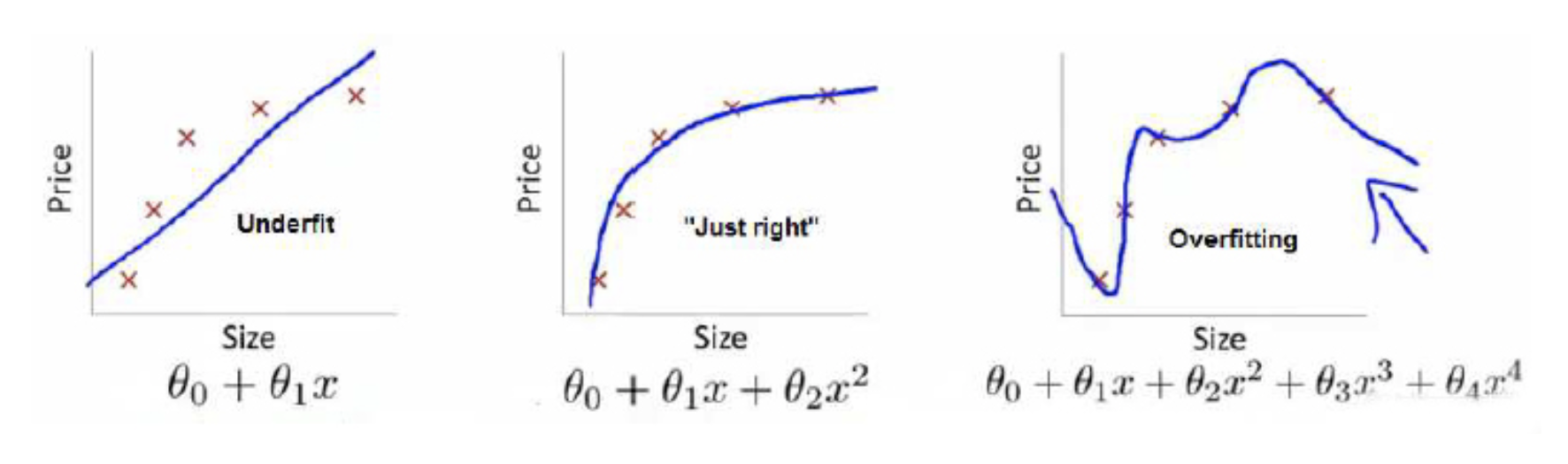
上面三个图的函数依次为 $f_1(x)$ , $f_2(x)$ , $f_3(x)$。
我们是想用这三个函数分别来拟合Price,Price的真实值记为$Y$。
我们给定$x$,这三个函数都会输出一个$f_(x)$,这个输出的$f_(x)$与真实值$Y$可能是相同的,也可能是不同的
为了表示我们拟合的好坏,我们就用一个函数来度量拟合的程度,比如:
$L(Y, f(X))= (Y-f(X))^2$,这个函数就称为损失函数(loss function),或者叫代价函数(cost function)
损失函数越小,就代表模型拟合的越好。那是不是我们的目标就只是让loss function越小越好呢?还不是。
这个时候还有一个概念叫风险函数(risk function)
风险函数是损失函数的期望,这是由于我们输入输出的$(X,Y)$遵循一个联合分布,但是这个联合分布是未知的,所以无法计算。
但是我们是有历史数据的,就是我们的训练集,$f(X)$关于训练集的平均损失称作经验风险(empirical risk),即$\frac{1}{N}\sum_{i=1}^\infty L(y_i,f(x_i))$,所以我们的目标就是最小化$\frac{1}{N}\sum_{i=1}^\infty L(y_i,f(x_i))$,称为经验风险最小化。
如果到这一步就完了的话,那我们看上面的图,那肯定是最右面的$f_3(x)$的经验风险函数最小了,因为它对历史的数据拟合的最好嘛。但是我们从图上来看$f_3(x)$肯定不是最好的,因为它过度学习历史数据,导致它在真正预测时效果会很不好,这种情况称为过拟合(over-fitting)。
它的函数太复杂了,都有四次方了,这就引出了下面的概念,我们不仅要让经验风险最小化,还要让结构风险最小化。这个时候就定义了一个函数$J(f)$ ,这个函数专门用来度量模型的复杂度,在机器学习中也叫正则化(regularization) 。常用的有$L1$, $L2$ 范数。
到这一步我们就可以说我们最终的优化函数是:$min\frac{1}{N}\sum_{i=1}^\infty L(y_i,f(x_i))+\lambda J(f)$ ,即最优化经验风险和结构风险,而这个函数就被称为目标函数。
结合上面的例子来分析:
最左面的$f_1(x)$结构风险最小(模型结构最简单),但是经验风险最大(对历史数据拟合的最差);最右面的$f_3(x)$经验风险最小(对历史数据拟合的最好),但是结构风险最大(模型结构最复杂);而$f_2(x)$达到了二者的良好平衡,最适合用来预测未知数据集。
forward by https://www.zhihu.com/question/52398145
欠拟合和过拟合
欠拟合和过拟合在机器学习中经常会出现,这里总结一下出现欠拟合和过拟合的原因、情形和解决方法。
过拟合和欠拟合是用于描述模型在训练过程中的两种状态,一般用来度量泛化能力的好坏。
作为比较,下图表示正常模型的表现:
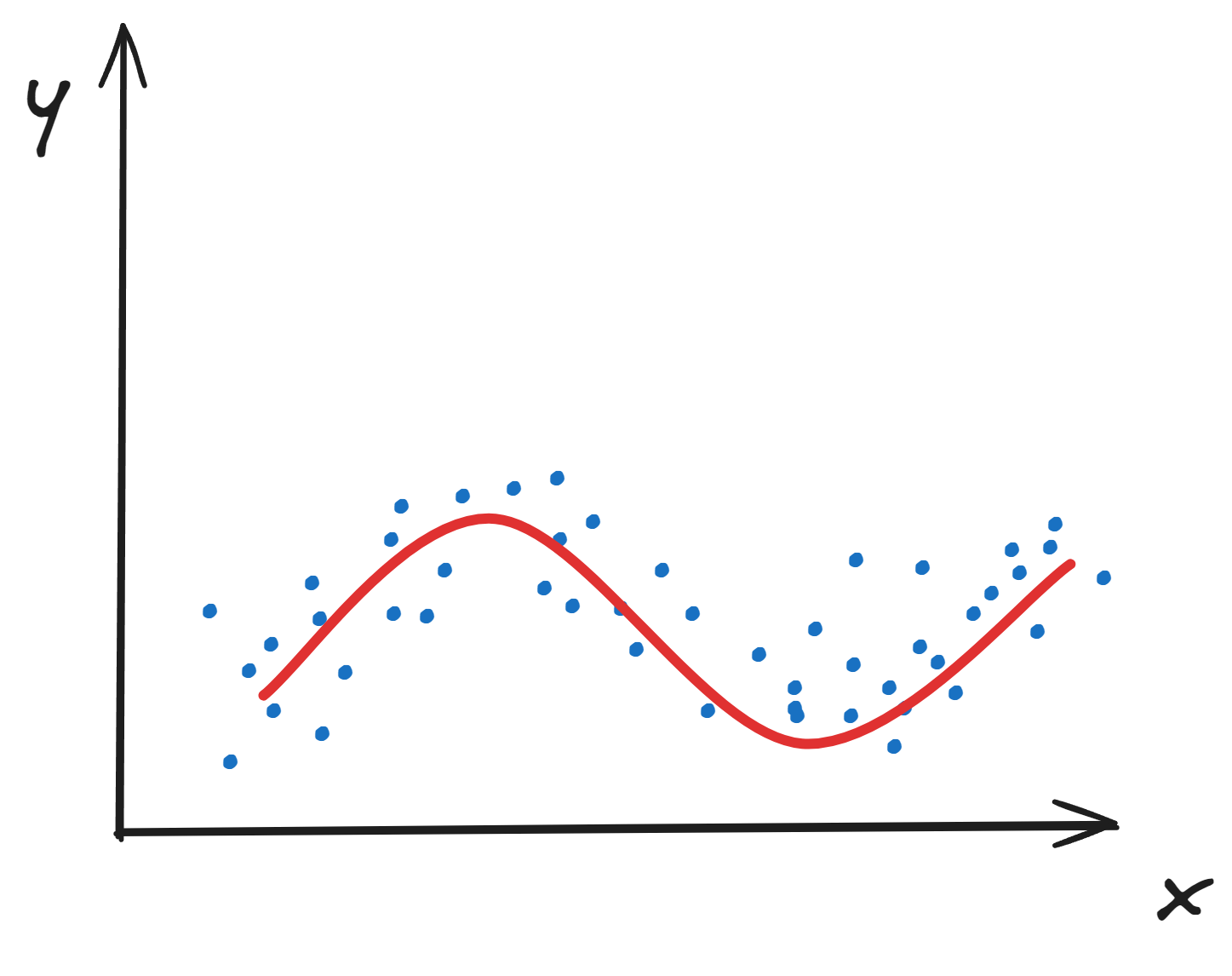
欠拟合 underfitting
欠拟合指的是模型在训练数据集和测试数据集上都变现不够好的情况。呈现出对训练数据没有很好的学习到数据特征。
欠拟合模型表现如下图所示:
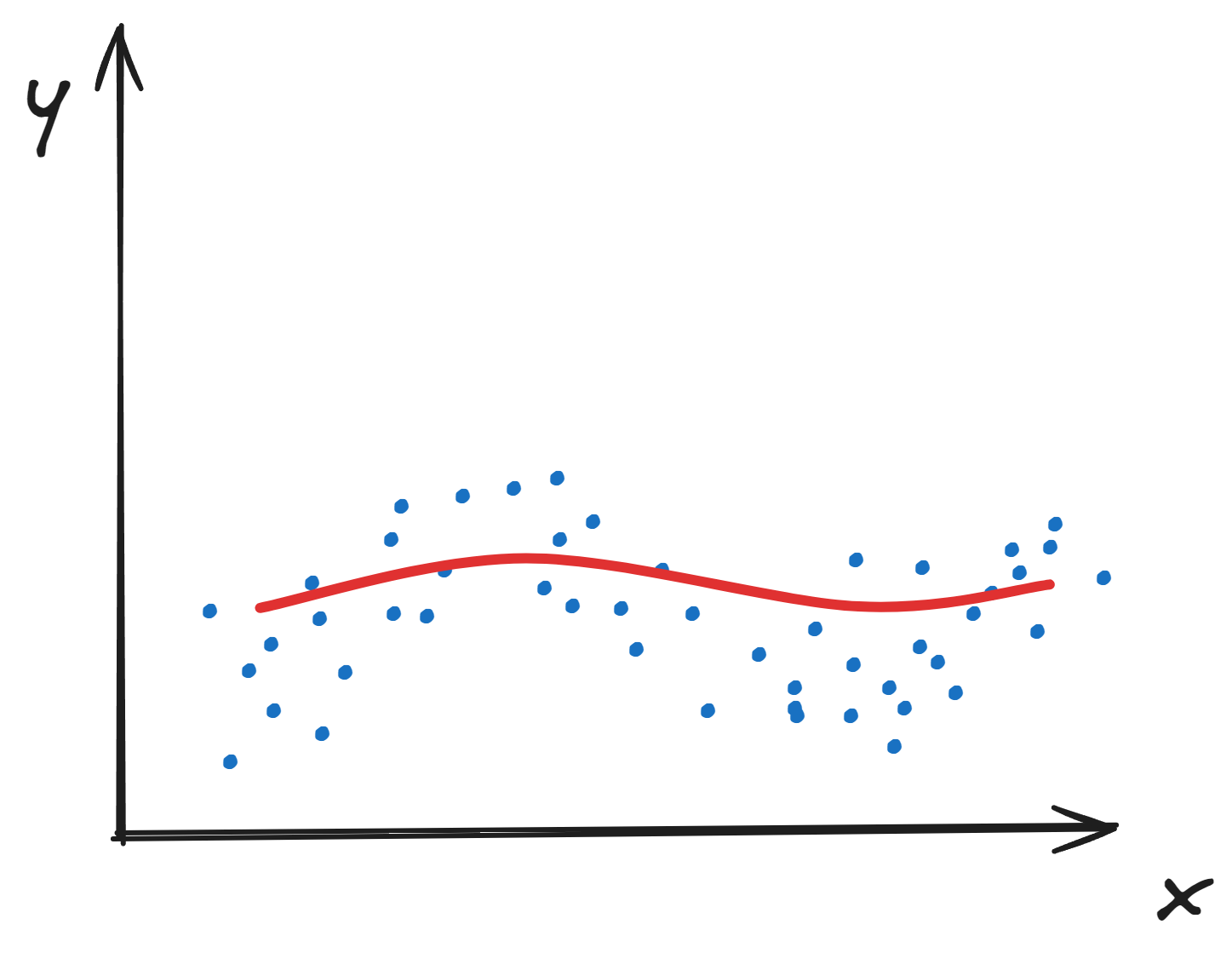
降低欠拟合的方法:
- 添加新特征。一般来说,欠拟合可能是因为对数据特征的挖掘不够,这时候,可以加强数据处理。通过人为的挖掘上下文特征、组合特征等。而在深度学习中,这一部分往往是模型自动完成了特征多样化的过程。
- 增加模型复杂度。模型的复杂度过于简单往往也会造成欠拟合的结果。简单的模型不能模拟出复杂的数据特征和行为,所以这时候就需要增加模型的复杂度。
- 降低正则化系数。正则化一般是用来防止模型过拟合的,如果模型出现欠拟合,可以适当的降低正则化系数。
过拟合 overfitting
过拟合指的是模型在训练数据集上表现的很好,但是在测试集上表现较差。呈现出对训练数据拟合过度了,所以叫过拟合。
过拟合模型表现如下图所示:
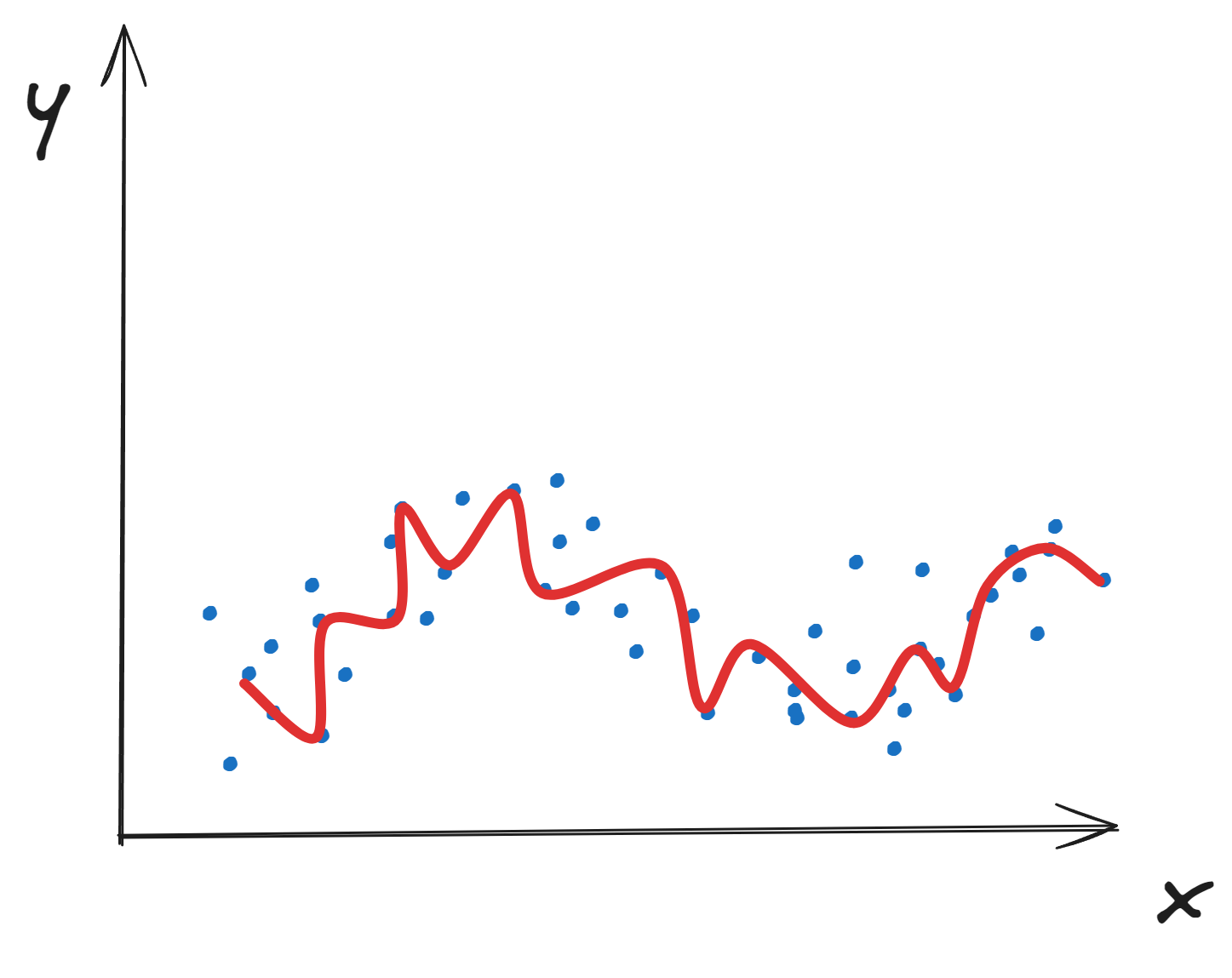
降低过拟合的方法:
- 增加训练集。数据集越多,一般来说模型表现的越好。
- 降低模型复杂度。和欠拟合相反,模型的复杂度过于复杂往往也会造成过拟合的结果。
- 增加正则化系数。正则化一般是用来防止模型过拟合的,如果模型出现过拟合,可以在模型中添加正则约束。如果已经有了,则可以适当上调正则化系数。
- 集成学习。为了防止单一模型过拟合,可以把多个模型集成在一起。
- Dropout,随机失活
梯度消失和梯度爆炸
梯度消失
梯度消失的根源是:深度神经网络和反向传播
反向传播:目前神经网络的优化方法大都基于反向传播的思想,即根据loss函数的误差通过梯度反向传播的方式指导深度神经网络的优化。
一般导致梯度消失的原因是在深层网络中使用了sigmoid等不合适的激活函数。
例如:在4层的全连接网络中,第$i$层网络激活($f$为激活函数)后的输出为$f_i(x)$,则$f_{i+1}=f(f_i*w_{i+1}+b_{i+1})$
基于梯度下降的优化策略,假设学习率为$\alpha$,得到参数更新为$\Delta w=-\alpha \frac {\partial Loss}{\partial w}$
根据链式求导法则,得到其上一层中更新梯度$\Delta w_2=-\alpha \frac {\partial Loss}{\partial w_2}=-\alpha \frac {\partial Loss}{\partial f_4}\frac {\partial f_4}{\partial f_3}\frac {\partial f_3}{\partial f_2}\frac {\partial f_2}{\partial w_2}$,其中$\frac {\partial f_4}{\partial f_3}$就是对激活函数的求导。
重点来了,如果这个值<1,那么随着层数的增加,经过很多次乘积后,就会导致其值无限趋近于0,即梯度消失。
梯度爆炸
原理同上,当激活函数求导后的值>1时,随着层数的增加,经过很多次乘积后,就会导致其值无限大,即梯度爆炸。
激活函数:
根据上面的原理,当激活为sigmoid时,其倒数是恒<=0.25的,所以当网络层数很多时,很容易导致梯度消失。sigmoid的函数为:$sigmoid(x)=\frac {1}{1+e^{-x}}$
另外,激活函数$tanh(x)$的导数恒<=1,也存在梯度消失问题。
解决方案:
- 使用Relu、leakRelu、elu等激活函数
- batchnorm(batch normalization)
- 残差结构
- LSTM
- 预训练加微调
- 梯度剪枝、权重正则(仅针对梯度爆炸)