AI安全 机器学习

机器学习全景：从数据预处理到算法调优的详细介绍

探索机器学习项目的每个步骤，深入解析数据预处理、算法选择与性能评估

Posted by Yewbs on August 31, 2019

Title: The Iron Rolling Mill (Modern Cyclopes)
Creator: Adolph Menzel
Date Created: 1872 - 1875
Physical Dimensions: w254.0 x h158.0 cm
Type: Painting
Technique and material: Oil on canvas
Inv.-No.: A I 201
ISIL-No.: DE-MUS-815114
External link: Alte Nationalgalerie, Staatliche Museen zu Berlin
Collection: Nationalgalerie, Staatliche Museen zu Berlin
Artist Place of Death: Berlin, Germany
Artist Place of Birth: Breslau, Poland
Artist Dates: 1815-12-08/1905-02-09

前言

在当今数据驱动的时代，机器学习正迅速成为各行业转型的核心动力。无论是从数据中提取洞察，还是构建智能系统，了解机器学习项目的全流程至关重要。本文将深入了解机器学习项目的一般步骤，从数据预处理到算法选择，再到神经网络的多样性与调参技巧，最后讨论如何有效评估模型性能。

机器学习项目流程

机器学习项目的一般步骤如下：

确定问题和目的

  • 明确项目的目标和需求，确定问题的类型（分类、回归、聚类等）。

收集数据

  • 收集相关数据，数据源可以是数据库、API、文件或网络爬虫。
  • 确保数据的质量和相关性。

数据预处理

  • 数据清洗：处理缺失值、异常值和重复数据。
  • 数据转换：标准化、归一化、编码分类变量等。
  • 特征选择：选择对模型有意义的特征，可能使用降维技术。

探索性数据分析 (EDA)

  • 使用可视化工具和统计方法分析数据的分布、趋势和关系。
  • 识别数据中的模式和特征。

选择算法

  • 根据问题类型、数据特征和项目要求选择合适的机器学习算法。

划分数据集

  • 将数据集划分为训练集、验证集和测试集，通常的比例为70%训练，15%验证，15%测试。

模型训练

  • 使用训练集对选择的算法进行训练，调整算法参数以优化模型性能。

结果评估

  • 使用验证集评估模型性能，选择适当的评估指标（如准确率、F1分数、均方误差等）。
  • 进行超参数调优以进一步提升模型性能。

模型测试

  • 使用测试集对最终模型进行评估，确保模型在未见数据上的泛化能力。

部署模型

  • 将训练好的模型部署到生产环境，可能涉及API开发或集成到现有系统中。
  • 确保模型可以实时接收输入并返回预测结果。

监控与维护

  • 监控模型在实际应用中的表现，及时发现和修正问题。
  • 定期更新模型以应对数据分布的变化或新数据的引入。

文档与报告

  • 记录项目的所有步骤、决策和结果，撰写报告以总结项目经验和发现。

通过遵循这些步骤，可以有效地管理和实施机器学习项目，确保项目的成功和可持续性。

下面我将介绍一些数据预处理、机器学习、神经网络以及如何调参的常见方法，最后介绍如何对机器学习的结果进行评估。

数据预处理

数据预处理是机器学习项目中至关重要的一步，主要包括数据清洗、转换和特征工程等。以下是一些常见的数据预处理方法的详细介绍：

数据清洗

  • 处理缺失值：
    • 删除法：直接删除包含缺失值的样本或特征。
    • 填充法：使用均值、中位数、众数或其他统计量填充缺失值。对于时间序列数据，可以使用前一个或后一个值填充（前向填充或后向填充）。
    • 插值法：使用插值技术根据其他值估算缺失值（例如线性插值）。
  • 处理异常值：
    • 统计方法：使用Z-score或IQR（四分位数间距）方法识别并处理异常值。
    • 替换法：将异常值替换为合理的值（如均值或中位数）。
  • 去重：
    • 检查并删除重复的记录，以确保数据的唯一性。

数据转换

  • 标准化：
    • 将特征缩放到均值为0，标准差为1的分布，常用于算法如支持向量机、K近邻等。
    • 公式：( z = \frac{x - \mu}{\sigma} )
  • 归一化：
    • 将特征缩放到特定的范围（如0到1），适用于神经网络等需要归一化输入的算法。
    • 公式：( x’ = \frac{x - \min(x)}{\max(x) - \min(x)} )
  • 编码分类变量：
    • 独热编码 (One-Hot Encoding)：将分类变量转换为二进制向量，适用于无序类别。
    • 标签编码 (Label Encoding)：将类别转换为整数，适用于有序类别。
  • 特征缩放：
    • 对数变换、平方根变换等，用于减小异常值的影响和提高数据的正态性。

特征工程

  • 特征选择：
    • 过滤法：使用统计测试（如卡方检验、相关系数）选择特征。
    • 包裹法：使用模型的性能作为特征选择的依据（如递归特征消除）。
    • 嵌入法：结合模型训练过程进行特征选择（如Lasso回归）。
  • 特征提取：
    • 主成分分析 (PCA)：通过线性变换将数据转换为少量主成分，减少维度。
    • 线性判别分析 (LDA)：用于分类任务的特征提取，最大化类别间距。
    • 自编码器：一种神经网络结构，学习数据的低维表示。
  • 特征构造：
    • 通过组合现有特征创建新特征（如多项式特征、交互特征）。
    • 处理时间序列数据时，提取时间特征（如年、月、日、小时等）。

数据集成

  • 合并数据集：
    • 将来自不同来源的数据集合并为一个完整的数据集，可能需要解决数据冗余和一致性问题。
  • 数据清洗和整合：
    • 确保数据在合并后的一致性和准确性，处理潜在的冲突和不一致。

样本平衡

  • 过采样和欠采样：
    • 在分类任务中，对于不平衡的数据集，可以采用过采样（如SMOTE算法）或欠采样技术来平衡类别。
  • 合成样本生成：
    • 生成新的样本以提高模型的泛化能力。

这些数据预处理方法可以帮助提高机器学习模型的性能，确保数据质量和适用性，为后续的建模过程打下良好的基础。

传统机器学习算法

机器学习算法是用于从数据中学习规律并进行预测或决策的模型。根据不同的学习方式，机器学习算法一般可以分为三大类：监督学习、无监督学习和强化学习。下面详细介绍这些类别及其常见算法。

监督学习

监督学习是指通过使用带标签的数据进行训练，从而预测未见数据的输出。常见的算法包括：

线性回归 (Linear Regression)

  • 用途：用于回归问题，预测连续数值。
  • 原理：假设因变量与自变量之间存在线性关系，通过最小二乘法找到最佳拟合线。

逻辑回归 (Logistic Regression)

  • 用途：用于二分类问题。
  • 原理：使用逻辑函数（Sigmoid函数）将输出映射到0和1之间，通过最大化似然估计进行训练。

决策树 (Decision Trees)

  • 用途：用于分类和回归任务。
  • 原理：通过特征划分构建树形结构，从根节点到叶节点的路径代表决策过程。

随机森林 (Random Forest)

  • 用途：用于分类和回归。
  • 原理：基于决策树的集成学习方法，通过构建多棵决策树并集成它们的结果来提高准确性。

支持向量机 (Support Vector Machines, SVM)

  • 用途：用于分类和回归。
  • 原理：通过寻找最佳超平面将数据划分为不同类别，最大化类别间的间隔。

K近邻算法 (K-Nearest Neighbors, KNN)

  • 用途：用于分类和回归。
  • 原理：通过计算新样本与训练样本之间的距离，选择距离最近的K个邻居进行投票或平均。

无监督学习

无监督学习是指在没有标签的数据中寻找模式或结构。常见的算法包括：

K均值聚类 (K-Means Clustering)

  • 用途：用于数据聚类。
  • 原理：将数据分为K个簇，通过迭代更新簇的中心点，最小化簇内样本的距离。

层次聚类 (Hierarchical Clustering)

  • 用途：用于数据聚类。
  • 原理：通过构建树形结构（树状图）表示数据的层次关系，可以是自底向上或自顶向下的方法。

主成分分析 (Principal Component Analysis, PCA)

  • 用途：用于降维和特征提取。
  • 原理：通过线性变换将数据投影到少量主成分上，最大化数据的方差。

自编码器 (Autoencoders)

  • 用途：用于特征学习和数据降维。
  • 原理：通过神经网络结构学习输入数据的低维表示，通常包括编码器和解码器两个部分。

神经网络算法

神经网络的种类越来越多，可以说是在呈指数级地增长。我们需要一个一目了然的图表，在这些新出现的网络构架和方法之间进行导航。本节内容原文链接：The mostly complete chart of Neural Networks, explained

来自Asimov研究所的Fjodor van Veen编写了一个关于神经网络的精彩图表：

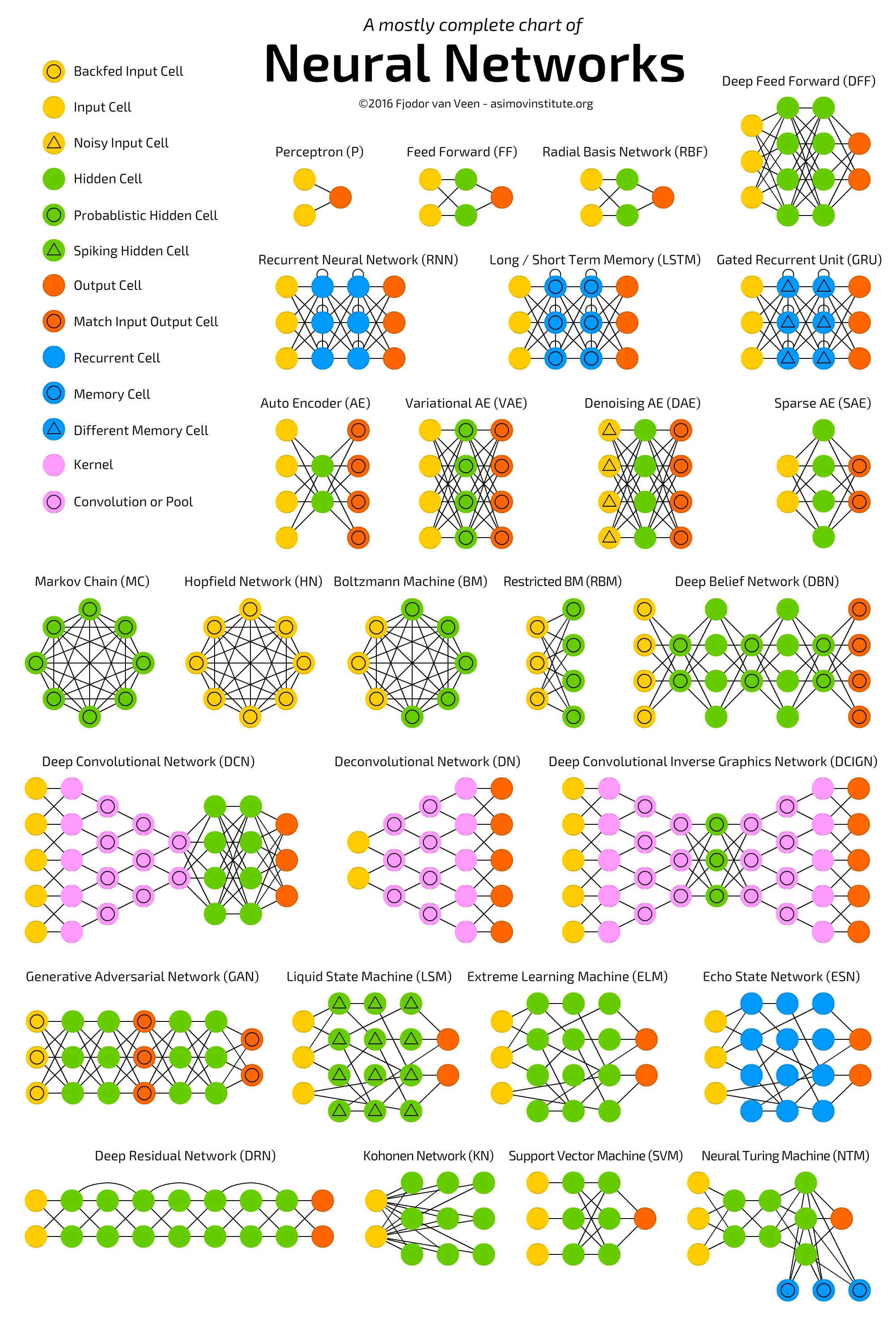
image.png

下面，我们就来逐一看看图中的27种神经网络：

Perceptron 感知机

image.png

Perceptron 感知机，我们知道的最简单和最古老的神经元模型。接收一些输入，把它们加总，通过激活函数并传递到输出层。这没什么神奇的地方。

前馈神经网络（FF）

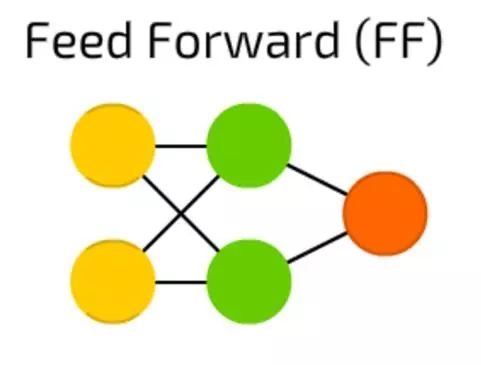
image.png

前馈神经网络（FF），这也是一个很古老的方法——这种方法起源于50年代。它的工作原理通常遵循以下规则：

  1. 所有节点都完全连接
  2. 激活从输入层流向输出，无回环
  3. 输入和输出之间有一层（隐含层）

在大多数情况下，这种类型的网络使用反向传播方法进行训练。

RBF 神经网络

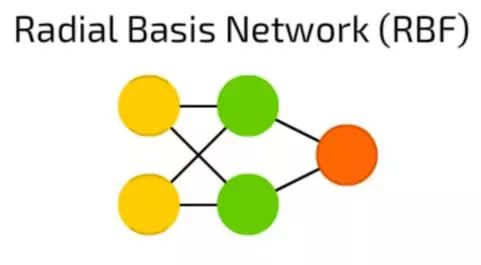
image.png

RBF 神经网络实际上是激活函数，是径向基函数而非逻辑函数的FF前馈神经网络。两者之间有什么区别呢？

逻辑函数将某个任意值映射到[0 ,… 1]范围内来，回答“是或否”问题。适用于分类决策系统，但不适用于连续变量。

相反，径向基函数能显示“我们距离目标有多远”。 这完美适用于函数逼近和机器控制（例如作为PID控制器的替代）。

简而言之，这些只是具有不同激活函数和应用方向的前馈网络。

DFF深度前馈神经网络

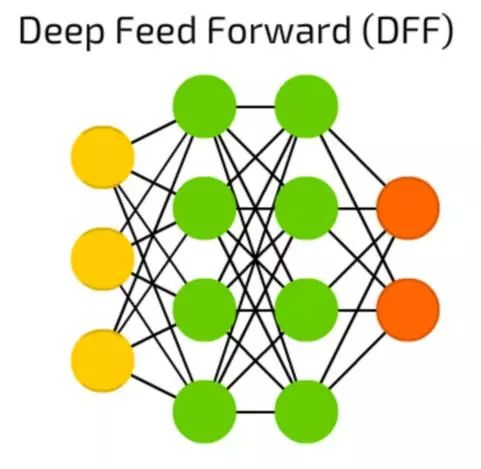
image.png

DFF深度前馈神经网络在90年代初期开启了深度学习的潘多拉盒子。这些依然是前馈神经网络，但有不止一个隐含层。那么，它到底有什么特殊性？

在训练传统的前馈神经网络时，我们只向上一层传递了少量的误差信息。由于堆叠更多的层次导致训练时间的指数增长，使得深度前馈神经网络非常不实用。

直到00年代初，我们开发了一系列有效的训练深度前馈神经网络的方法；现在它们构成了现代机器学习系统的核心，能实现前馈神经网络的功能，但效果远高于此。

RNN递归神经网络

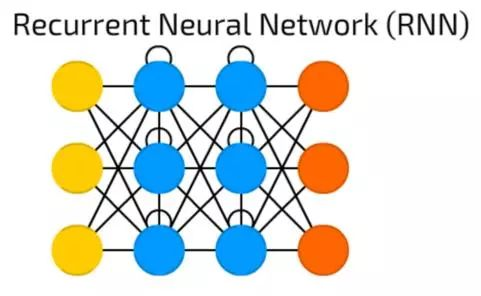
image.png

RNN递归神经网络引入不同类型的神经元——递归神经元。这种类型的第一个网络被称为约旦网络（Jordan Network），在网络中每个隐含神经元会收到它自己的在固定延迟（一次或多次迭代）后的输出。除此之外，它与普通的模糊神经网络非常相似。

当然，它有许多变化  —  如传递状态到输入节点，可变延迟等，但主要思想保持不变。这种类型的神经网络主要被使用在上下文很重要的时候——即过去的迭代结果和样本产生的决策会对当前产生影响。最常见的上下文的例子是文本——一个单词只能在前面的单词或句子的上下文中进行分析。

LSTM长短时记忆网络

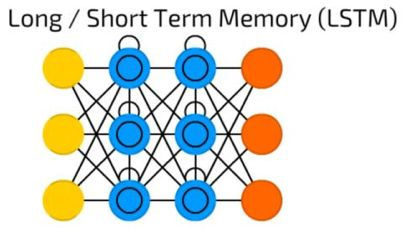
image.png

LSTM长短时记忆网络引入了一个存储单元，一个特殊的单元，当数据有时间间隔（或滞后）时可以处理数据。递归神经网络可以通过“记住”前十个词来处理文本，LSTM长短时记忆网络可以通过“记住”许多帧之前发生的事情处理视频帧。 LSTM网络也广泛用于写作和语音识别。

存储单元实际上由一些元素组成，称为门，它们是递归性的，并控制信息如何被记住和遗忘。下图很好的解释了LSTM的结构:

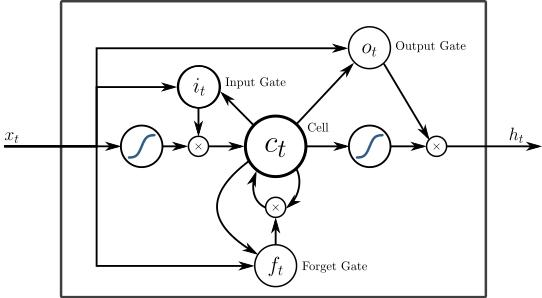
image.png

上图的（x）是门，他们拥有自己的权重，有时也有激活函数。在每个样本上，他们决定是否传递数据，擦除记忆等等 - 你可以在这里阅读更详细的解释。 输入门(Input Gate)决定上一个样本有多少的信息将保存在内存中; 输出门调节传输到下一层的数据量，遗忘门(Forget Gate)控制存储记忆的损失率。

然而，这是LSTM单元的一个非常简单的实现，还有许多其他架构存在。

GRU

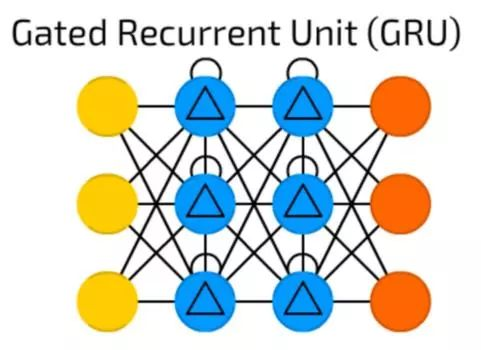
image.png

GRU是具有不同门的LSTM。

听起来很简单，但缺少输出门可以更容易基于具体输入重复多次相同的输出，目前此模型在声音（音乐）和语音合成中使用得最多。

实际上的组合虽然有点不同：但是所有的LSTM门都被组合成所谓的更新门(Update Gate)，并且复位门(Reset Gate)与输入密切相关。

它们比LSTM消耗资源少，但几乎有相同的效果。

Autoencoders自动编码器

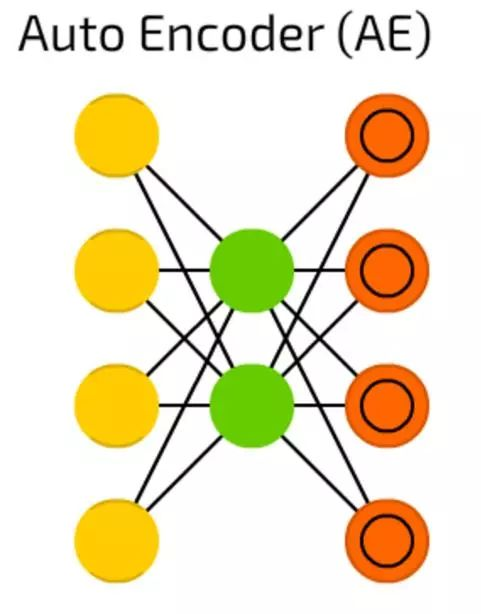
image.png

Autoencoders自动编码器用于分类，聚类和特征压缩。

当您训练前馈(FF)神经网络进行分类时，您主要必须在Y类别中提供X个示例，并且期望Y个输出单元格中的一个被激活。 这被称为“监督学习”。

另一方面，自动编码器可以在没有监督的情况下进行训练。它们的结构 - 当隐藏单元数量小于输入单元数量（并且输出单元数量等于输入单元数）时，并且当自动编码器被训练时输出尽可能接近输入的方式，强制自动编码器泛化数据并搜索常见模式。

变分自编码器

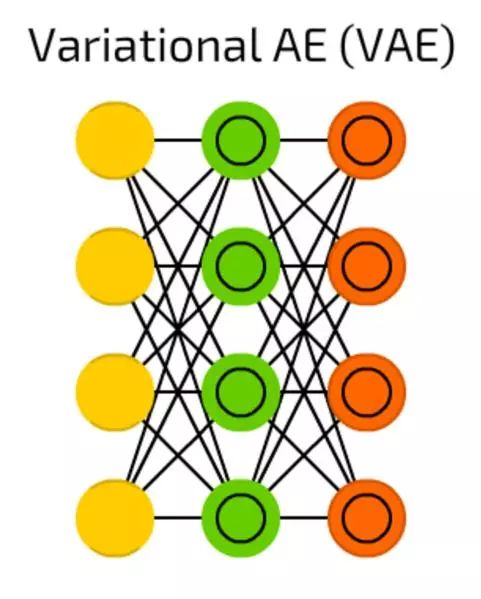
image.png

变分自编码器，与一般自编码器相比，它压缩的是概率，而不是特征。

尽管如此简单的改变，但是一般自编码器只能回答当“我们如何归纳数据？”的问题时，变分自编码器回答了“两件事情之间的联系有多强大？我们应该在两件事情之间分配误差还是它们完全独立的？”的问题。

在这里可以看到一些更深入的解释（含代码示例）。

降噪自动编码器（DAE）

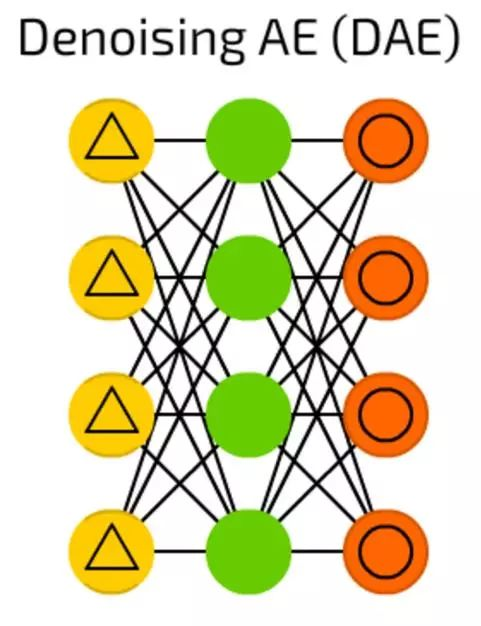
image.png

虽然自动编码器很酷，但它们有时找不到最鲁棒的特征，而只是适应输入数据（实际上是过拟合的一个例子）。

降噪自动编码器（DAE）在输入单元上增加了一些噪声 - 通过随机位来改变数据，随机切换输入中的位，等等。通过这样做，一个强制降噪自动编码器从一个有点嘈杂的输入重构输出，使其更加通用，强制选择更常见的特征。

稀疏自编码器（SAE）

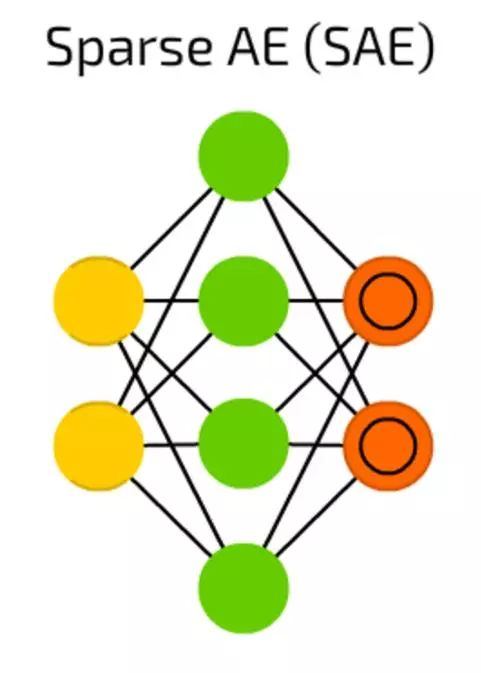
image.png

稀疏自编码器（SAE）是另外一个有时候可以抽离出数据中一些隐藏分组样试的自动编码的形式。结构和AE是一样的，但隐藏单元的数量大于输入或输出单元的数量。

马尔可夫链（Markov Chain, MC）

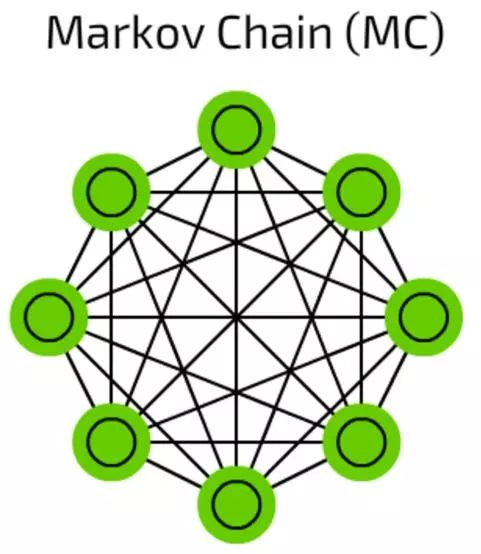
image.png

马尔可夫链（Markov Chain, MC）是一个比较老的图表概念了，它的每一个端点都存在一种可能性。过去，我们用它来搭建像“在单词hello之后有0.0053％的概率会出现dear，有0.03551%的概率出现you”这样的文本结构。

这些马尔科夫链并不是典型的神经网络，它可以被用作基于概率的分类（像贝叶斯过滤），用于聚类（对某些类别而言），也被用作有限状态机。

霍普菲尔网络（HN）

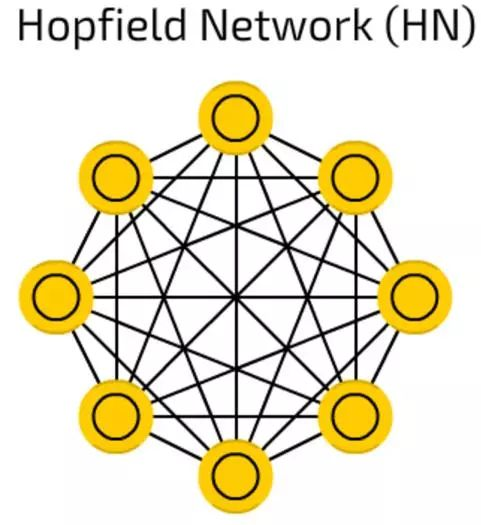
image.png

霍普菲尔网络（HN）对一套有限的样本进行训练，所以它们用相同的样本对已知样本作出反应。

在训练前，每一个样本都作为输入样本，在训练之中作为隐藏样本，使用过之后被用作输出样本。

在HN试着重构受训样本的时候，他们可以用于给输入值降噪和修复输入。如果给出一半图片或数列用来学习，它们可以反馈全部样本。

波尔滋曼机（BM）

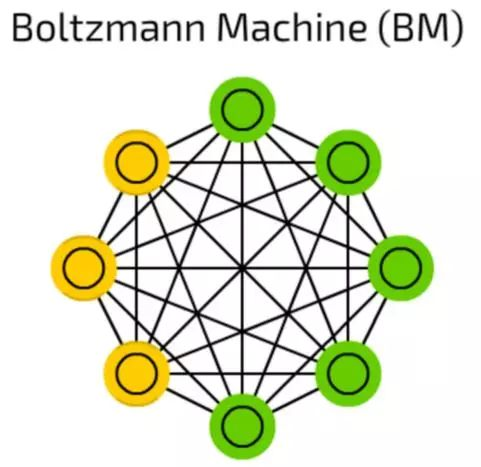
image.png

波尔滋曼机（BM）和HN非常相像，有些单元被标记为输入同时也是隐藏单元。在隐藏单元更新其状态时，输入单元就变成了输出单元。（在训练时，BM和HN一个一个的更新单元，而非并行）。

多层叠的波尔滋曼机可以用于所谓的深度信念网络（等一下会介绍），深度信念网络可以用作特征检测和抽取。

限制型波尔滋曼机（RBM）

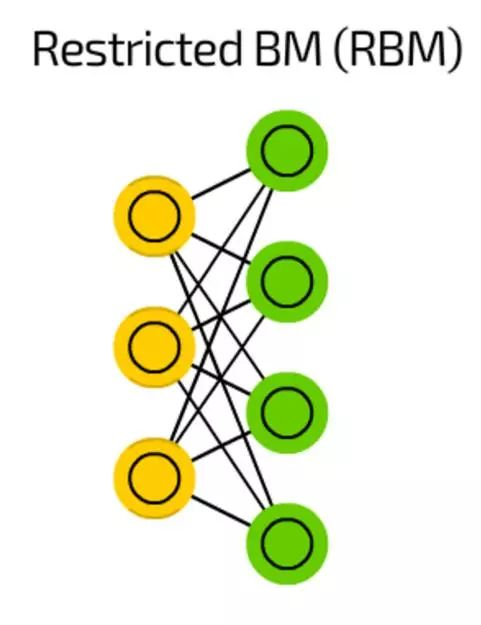
image.png

在结构上，限制型波尔滋曼机（RBM）和BM很相似，但由于受限RBM被允许像FF一样用反向传播来训练（唯一的不同的是在反向传播经过数据之前RBM会经过一次输入层）。

深度信念网络（DBN）

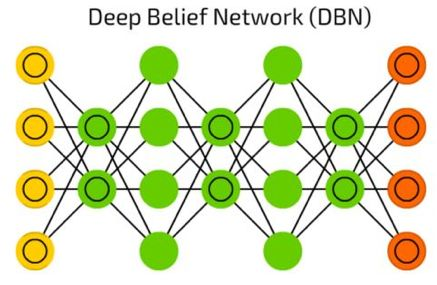
image.png

像之前提到的那样，深度信念网络（DBN）实际上是许多波尔滋曼机（被VAE包围）。他们能被连在一起（在一个神经网络训练另一个的时候），并且可以用已经学习过的样式来生成数据。

深度卷积网络（DCN）

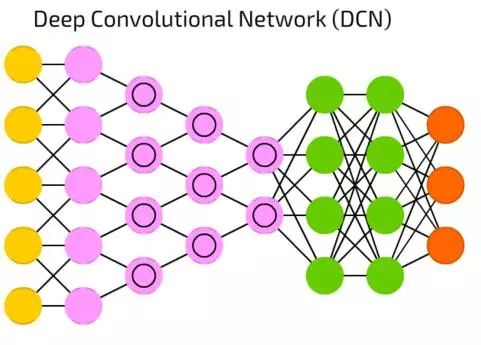
image.png

当今，深度卷积网络（DCN）是人工神经网络之星。它具有卷积单元（或者池化层）和内核，每一种都用以不同目的。

卷积核事实上用来处理输入的数据，池化层是用来简化它们（大多数情况是用非线性方程，比如max），来减少不必要的特征。

他们通常被用来做图像识别，它们在图片的一小部分上运行（大约20x20像素）。输入窗口一个像素一个像素的沿着图像滑动。然后数据流向卷积层，卷积层形成一个漏斗（压缩被识别的特征）。从图像识别来讲，第一层识别梯度，第二层识别线，第三层识别形状，以此类推，直到特定的物体那一级。DFF通常被接在卷积层的末端方便未来的数据处理。

去卷积网络（DN）

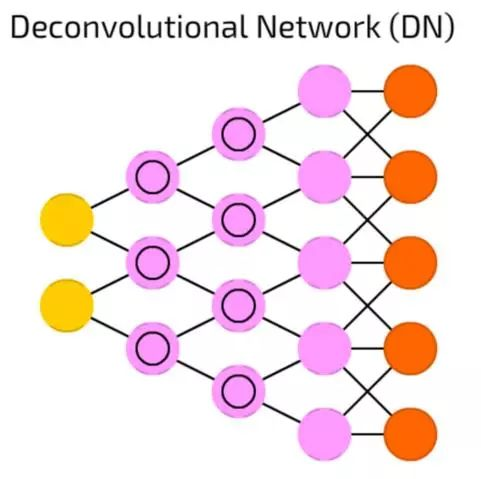
image.png

去卷积网络（DN）是将DCN颠倒过来。DN能在获取猫的图片之后生成像（狗：0，蜥蜴：0，马：0，猫：1）一样的向量。DNC能在得到这个向量之后，能画出一只猫。

深度卷积反转图像网络（DCIGN）

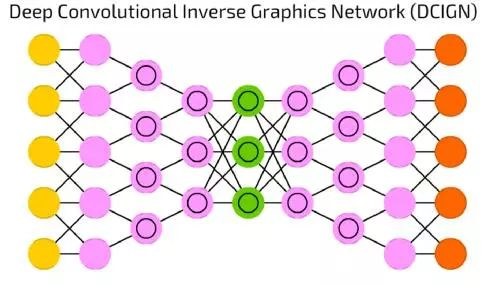
image.png

深度卷积反转图像网络（DCIGN），长得像DCN和DN粘在一起，但也不完全是这样。

事实上，它是一个自动编码器，DCN和DN并不是作为两个分开的网络，而是承载网路输入和输出的间隔区。大多数这种神经网络可以被用作图像处理，并且可以处理他们以前没有被训练过的图像。由于其抽象化的水平很高，这些网络可以用于将某个事物从一张图片中移除，重画，或者像大名鼎鼎的CycleGAN一样将一匹马换成一个斑马。

生成对抗网络（GAN）

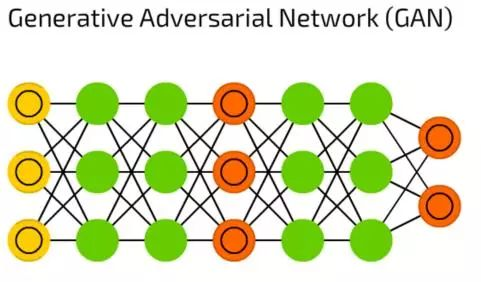
image.png

生成对抗网络（GAN）代表了有生成器和分辨器组成的双网络大家族。它们一直在相互伤害——生成器试着生成一些数据，而分辨器接收样本数据后试着分辨出哪些是样本，哪些是生成的。只要你能够保持两种神经网络训练之间的平衡，在不断的进化中，这种神经网络可以生成实际图像。

液体状态机（LSM）

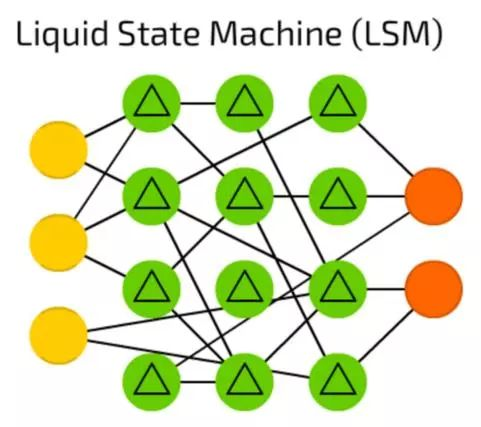
image.png

液体状态机（LSM）是一种稀疏的，激活函数被阈值代替了的（并不是全部相连的）神经网络。只有达到阈值的时候，单元格从连续的样本和释放出来的输出中积累价值信息，并再次将内部的副本设为零。

这种想法来自于人脑，这些神经网络被广泛的应用于计算机视觉，语音识别系统，但目前还没有重大突破。

极端学习机（ELM）

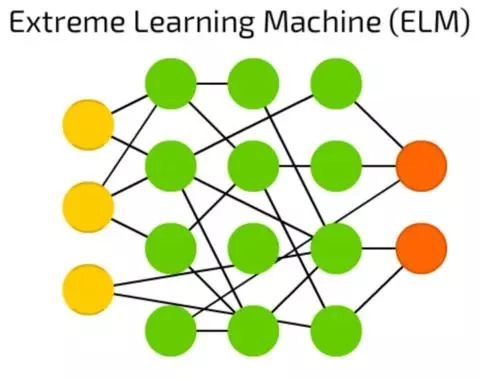
image.png

极端学习机（ELM）是通过产生稀疏的随机连接的隐藏层来减少FF网络背后的复杂性。它们需要用到更少计算机的能量，实际的效率很大程度上取决于任务和数据。

回声状态网络（ESN）

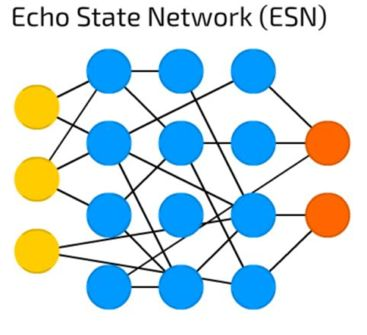
image.png

回声状态网络（ESN）是重复网络的细分种类。数据会经过输入端，如果被监测到进行了多次迭代（请允许重复网路的特征乱入一下），只有在隐藏层之间的权重会在此之后更新。

深度残差网络（DRN）

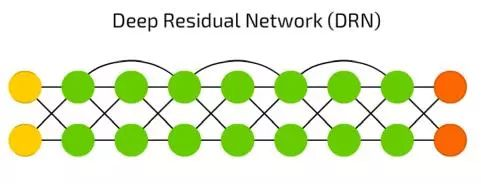
image.png

深度残差网络（DRN）是有些输入值的部分会传递到下一层。这一特点可以让它可以做到很深的层级（达到300层），但事实上它们是一种没有明确延时的RNN。

Kohonen神经网络（KN）

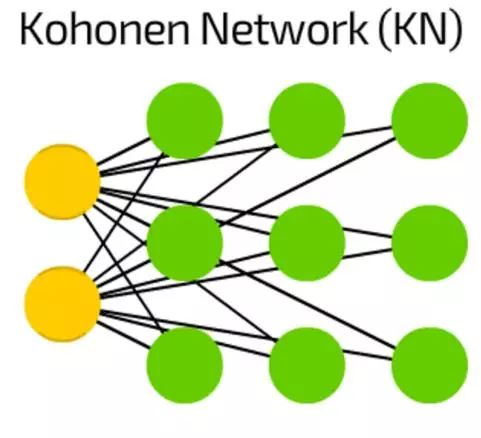
image.png

Kohonen神经网络（KN）引入了“单元格距离”的特征。大多数情况下用于分类，这种网络试着调整它们的单元格使其对某种特定的输入作出最可能的反应。当一些单元格更新了， 离他们最近的单元格也会更新。

像SVM一样，这些网络总被认为不是“真正”的神经网络。

支持向量机（SVM）

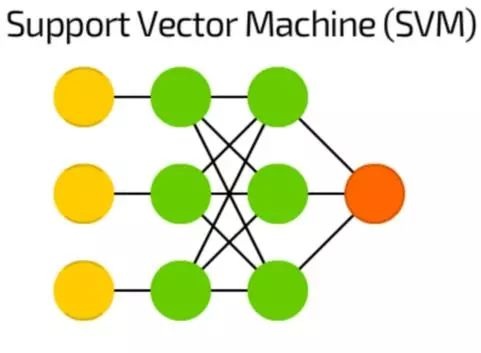
image.png

支持向量机（SVM）用于二元分类工作，无论这个网络处理多少维度或输入，结果都会是“是”或“否”。

SVM不是所有情况下都被叫做神经网络。

神经图灵机（NTM）

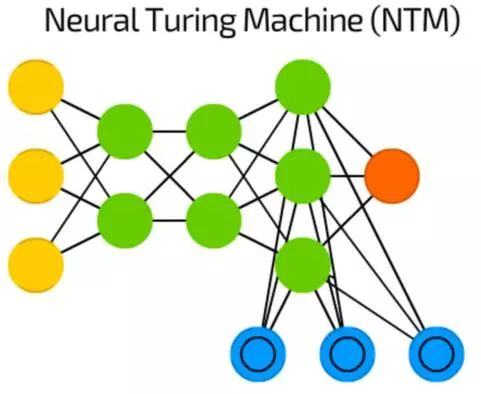
image.png

神经网络像是黑箱——我们可以训练它们，得到结果，增强它们，但实际的决定路径大多数我们都是不可见的。

神经图灵机（NTM）就是在尝试解决这个问题——它是一个提取出记忆单元之后的FF。一些作者也说它是一个抽象版的LSTM。

记忆是被内容编址的，这个网络可以基于现状读取记忆，编写记忆，也代表了图灵完备神经网络。

神经网络调参

梯度下降

梯度下降算法（Gradient Descent Optimization）是神经网络模型训练最常用的优化算法。对于深度学习模型，基本都是采用梯度下降算法来进行优化训练的。梯度下降算法背后的原理：目标函数关于参数的梯度将是目标函数上升最快的方向。对于最小化优化问题，只需要将参数沿着梯度相反的方向前进一个步长，就可以实现目标函数的下降。这个步长又称为学习速率 $\eta$ 。参数更新公式如下：

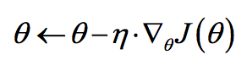
image.png

其中 $\nabla_{\theta}J(\theta)$ 是参数的梯度，根据计算目标函数$J(\theta)$ 采用数据量的不同，梯度下降算法又可以分为批量梯度下降算法（Batch Gradient Descent），随机梯度下降算法（Stochastic GradientDescent）和小批量梯度下降算法（Mini-batch Gradient Descent）。

对于批量梯度下降算法，其$J(\theta)$是在整个训练集上计算的，如果数据集比较大，可能会面临内存不足问题，而且其收敛速度一般比较慢。

随机梯度下降算法是另外一个极端，$J(\theta)$是针对训练集中的一个训练样本计算的，又称为在线学习，即得到了一个样本，就可以执行一次参数更新。所以其收敛速度会快一些，但是有可能出现目标函数值震荡现象，因为高频率的参数更新导致了高方差。

小批量梯度下降算法是折中方案，选取训练集中一个小批量样本计算$J(\theta)$，这样可以保证训练过程更稳定，而且采用批量训练方法也可以利用矩阵计算的优势。这是目前最常用的梯度下降算法。

对于神经网络模型，借助于BP算法可以高效地计算梯度，从而实施梯度下降算法。但梯度下降算法一个老大难的问题是：不能保证全局收敛。如果这个问题解决了，深度学习的世界会和谐很多。

梯度下降算法针对凸优化问题原则上是可以收敛到全局最优的，因为此时只有唯一的局部最优点。而实际上深度学习模型是一个复杂的非线性结构，一般属于非凸问题，这意味着存在很多局部最优点（鞍点），采用梯度下降算法可能会陷入局部最优，这应该是最头疼的问题。这点和进化算法如遗传算法很类似，都无法保证收敛到全局最优。

因此，我们注定在这个问题上成为“高级调参师”。可以看到，梯度下降算法中一个重要的参数是学习速率，适当的学习速率很重要：学习速率过小时收敛速度慢，而过大时导致训练震荡，而且可能会发散。

理想的梯度下降算法要满足两点：收敛速度要快；能全局收敛。为了这个理想，出现了很多经典梯度下降算法的变种，下面将分别介绍它们。

Momentum optimization

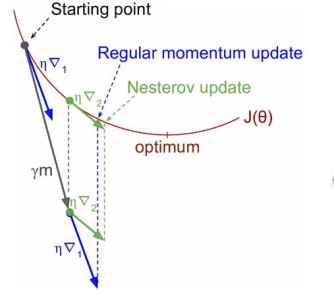
冲量梯度下降算法是BorisPolyak在1964年提出的，其基于这样一个物理事实：将一个小球从山顶滚下，其初始速率很慢，但在加速度作用下速率很快增加，并最终由于阻力的存在达到一个稳定速率。对于冲量梯度下降算法，其更新方程如下：

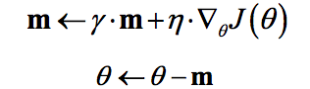
image.png

可以看到，参数更新时不仅考虑当前梯度值，而且加上了一个积累项（冲量），但多了一个超参$\gamma$，一般取接近1的值如0.9。相比原始梯度下降算法，冲量梯度下降算法有助于加速收敛。当梯度与冲量方向一致时，冲量项会增加，而相反时，冲量项减少，因此冲量梯度下降算法可以减少训练的震荡过程。TensorFlow中提供了这一优化器：

tf.train.MomentumOptimizer(learning_rate=learning_rate,momentum=0.9)。

NAG

NAG算法全称Nesterov Accelerated Gradient,是YuriiNesterov在1983年提出的对冲量梯度下降算法的改进版本，其速度更快。其变化之处在于计算“超前梯度”更新冲量项，具体公式如下：

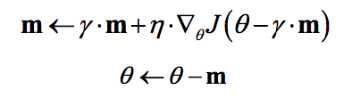
image.png

既然参数要沿着$\gamma \cdot m$更新，不妨计算未来位置$\theta - \gamma \cdot m$的梯度，然后合并两项作为最终的更新项，其具体效果如图1所示，可以看到一定的加速效果。在TensorFlow中，NAG优化器为：

tf.train.MomentumOptimizer(learning_rate=learning_rate,momentum=0.9, use_nesterov=True)

image.png

AdaGrad

AdaGrad是Duchi在2011年提出的一种学习速率自适应的梯度下降算法。在训练迭代过程，其学习速率是逐渐衰减的，经常更新的参数其学习速率衰减更快，这是一种自适应算法。其更新过程如下：

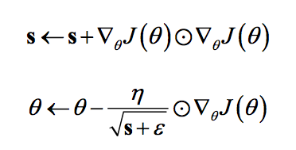
image.png

其中是梯度平方的积累量，在进行参数更新时，学习速率要除以这个积累量的平方根，其中加上一个很小值是为了防止除0的出现。由于是该项逐渐增加的，那么学习速率是衰减的。考虑如图2所示的情况，目标函数在两个方向的坡度不一样，如果是原始的梯度下降算法，在接近坡底时收敛速度比较慢。而当采用AdaGrad，这种情况可以被改观。由于比较陡的方向梯度比较大，其学习速率将衰减得更快，这有利于参数沿着更接近坡底的方向移动，从而加速收敛。

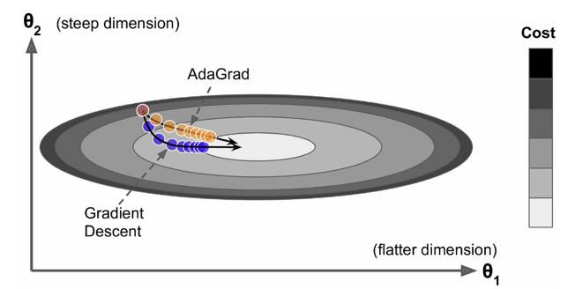
image.png

前面说到AdaGrad其学习速率实际上是不断衰减的，这会导致一个很大的问题，就是训练后期学习速率很小，导致训练过早停止，因此在实际中AdaGrad一般不会被采用，下面的算法将改进这一致命缺陷。不过TensorFlow也提供了这一优化器：tf.train.AdagradOptimizer。

RMSprop

RMSprop是Hinton在他的课程上讲到的，其算是对Adagrad算法的改进，主要是解决学习速率过快衰减的问题。其实思路很简单，类似Momentum思想，引入一个超参数，在积累梯度平方项进行衰减：

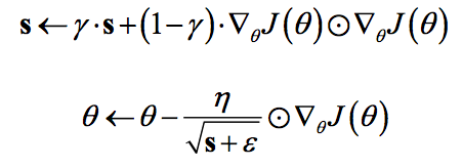
image.png

可以认为仅仅对距离时间较近的梯度进行积累，其中一般取值0.9，其实这样就是一个指数衰减的均值项，减少了出现的爆炸情况，因此有助于避免学习速率很快下降的问题。同时Hinton也建议学习速率设置为0.001。RMSprop是属于一种比较好的优化算法了，在TensorFlow中当然有其身影：

tf.train.RMSPropOptimizer(learning_rate=learning_rate,momentum=0.9, decay=0.9, epsilon=1e-10)。

不得不说点题外话，同时期还有一个Adadelta算法，其也是Adagrad算法的改进，而且改进思路和RMSprop很像，但是其背后是基于一次梯度近似代替二次梯度的思想，感兴趣的可以看看相应的论文，这里不再赘述。

Adam

Adam全称Adaptive moment estimation，是Kingma等在2015年提出的一种新的优化算法，其结合了Momentum和RMSprop算法的思想。相比Momentum算法，其学习速率是自适应的，而相比RMSprop，其增加了冲量项。所以，Adam是两者的结合体：

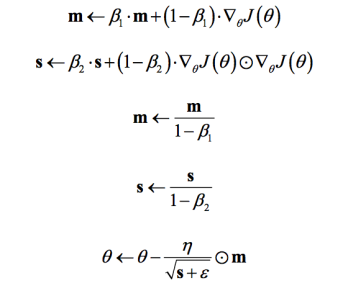
image.png

可以看到前两项和Momentum和RMSprop是非常一致的，由于和的初始值一般设置为0，在训练初期其可能较小，第三和第四项主要是为了放大它们。最后一项是参数更新。其中超参数的建议值是$\beta_{1}=0.9, \beta_{2}=0.999, \varepsilon=1e-8$。Adm是性能非常好的算法，在TensorFlow其实现如下：

tf.train.AdamOptimizer(learning_rate=0.001,beta1=0.9, beta2=0.999, epsilon=1e-08)。

学习速率

前面也说过学习速率的问题，对于梯度下降算法，这应该是一个最重要的超参数。如果学习速率设置得非常大，那么训练可能不会收敛，就直接发散了；如果设置的比较小，虽然可以收敛，但是训练时间可能无法接受；如果设置的稍微高一些，训练速度会很快，但是当接近最优点会发生震荡，甚至无法稳定。不同学习速率的选择影响可能非常大，如图所示。

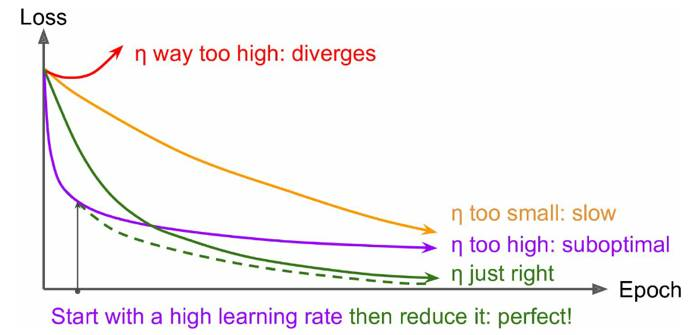
image.png

理想的学习速率是：刚开始设置较大，有很快的收敛速度，然后慢慢衰减，保证稳定到达最优点。所以，前面的很多算法都是学习速率自适应的。除此之外，还可以手动实现这样一个自适应过程，如实现学习速率指数式衰减：

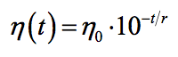
image.png

在TensorFlow中，你可以这样实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

initial_learning_rate = 0.1

decay_steps = 10000

decay_rate = 1/10

global_step = tf.Variable(0, trainable=False)

learning_rate = tf.train.exponential_decay(initial_learning_rate,

global_step, decay_steps, decay_rate)

# decayed_learning_rate = learning_rate *

# decay_rate ^ (global_step / decay_steps)

optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)

training_op = optimizer.minimize(loss, global_step=global_step)

总结来看，优先选择学习速率自适应的算法如RMSprop和Adam算法，大部分情况下其效果是较好的。还有一定要特别注意学习速率的问题。其实还有很多方面会影响梯度下降算法，如梯度的消失与爆炸，这也是要额外注意的。最后不得不说，梯度下降算法目前无法保证全局收敛还将是一个持续性的数学难题。

交叉熵及loss函数中使用

推荐文章：https://blog.csdn.net/tsyccnh/article/details/79163834

理解正则化

推荐文章：https://blog.csdn.net/yuweiming70/article/details/81513742

理解Softmax

推荐文章：https://blog.csdn.net/red_stone1/article/details/80687921

梯度消失及梯度爆炸

推荐文章：https://blog.csdn.net/qq_25737169/article/details/78847691

评价指标

假设原始样本中有两类，其中：总共有P个类别为1的样本，假设类别1为正例。总共有N个类别为0的样本，假设类别0为负例。

经过分类后，有 TP个类别为1的样本被系统正确判定为类别1，FN个类别为1的样本被系统误判定为类别 0，显然有P=TP+FN；有 FP个类别为0 的样本被系统误判断定为类别1，TN个类别为0的样本被系统正确判为类别 0，显然有N=FP+TN。相关术语定义如下：

  • 准确率（Accuracy）：Accuracy= (TP + TN)/(P+N) = (TP + TN)/(TP + FN + FP + TN)；反映了分类器统对整个样本的判定能力——能将正的判定为正，负的判定为负；
  • 精确率/查准率（Precision）：Precision= TP/(TP+FP)；反映了被分类器判定的正例中真正的正例样本的比重；
  • 召回率/查全率（Recall）：Recall= TP/(TP+FN) = 1 - FN/T；也称为True Positive Rate，反映了被正确判定的正例占总的正例的比重；
  • 误报率/假正率（False Positive Rate）：FPR = FP/N；将负类预测为正类数；
  • 漏报率/假负率（False Negative Rate）：FNR = FN/P；将正类预测为负类数。
  • EER（Equal Error Rate，等概率错误）：这个在说话人识别，说话人确认中最常用的评价标准，是一种使错误接受率nontarget_is_target / (target_is_target + nontarget_is_target) 和错误拒绝率target_is_nontarget / (target_is_nontarget + nontarget_is_nontarget)的一个相对平衡点阈值点，然后这个阈值点可以作为实际使用阶段的固定的阈值。
  • ROC曲线（ReceiverOperating Characteristic）：ROC曲线上每个点反映着对同一信号刺激的感受性。横轴：误报率/假正率(FPR)特异度，划分实例中所有负例占所有负例的比例；(1-Specificity)。纵轴：召回率/查全率(TPR)灵敏度，Sensitivity(正类覆盖率)。
CATALOG
    FEATURED TAGS
    网络安全 区块链 AI安全 CTF 密码学 区块链基础 机器学习 哈希函数 ETH 声纹识别 读书笔记 对称密码 数据分析 智能合约 AES python