Title: The Lady of Shalott
Creator: John William Waterhouse
Creator Lifespan: 1849/1917
Creator Death Place: London, United Kingdom
Creator Birth Place: Roma, Italia
Date Created: 1888
Provenance: Presented by Sir Henry Tate 1894
Physical Dimensions: w200 x h153 mm
Original Title: The Lady of Shalott
Type: Painting
Medium: Oil on Canvas
UBM 训练实验
In [1]:
1
2
3
4
5
import csv
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
参数设置
In [2]:
1
2
3
N = 1000 # 样本数
D = 13 # 特征数
K = 5 # 高斯数
读取MFCC
In [3]:
1
2
3
4
5
6
7
8
9
10
data = []
with open("aa.csv", "r") as f:
r = csv.reader(f, delimiter = ",")
for i, d in enumerate(r):
if i < N:
data.append(d)
else:
break
data = np.array(data).astype(np.float)
data.shape
Out[3]:
1
(1000, 13)
定义变量
In [4]:
1
2
3
4
z_n_k = np.zeros((N,K)) # 隐变量的后验概率
mu_k = np.zeros((K,D)) # 高斯均值
cov_k = np.zeros((K,D,D))# 协方差
pi_k = np.zeros((K,1)) # 均值矩阵
初始化 O(样本数*迭代次数)
In [5]:
1
2
3
4
5
6
7
8
9
def k_means(data,N,K,D,MAX_ITERATIONS): # O(样本数*迭代次数)
cov = np.zeros((K,D,D)) # 协方差
pi = np.zeros((K,1)) # 高斯权值
kmeans = KMeans(n_clusters = K).fit(data) # 寻找均值,高斯核中心
for k in range(K):
cov[k] = np.cov(data[kmeans.labels_ == k].T)
pi[k] = data[kmeans.labels_ == k].shape[0]/N
print("均值:{0},协方差:{1},权值{2}".format(kmeans.cluster_centers_.shape,cov.shape,pi.shape))
return kmeans.cluster_centers_,cov,pi
In [6]:
1
mu_k,cov_k,pi_k = k_means(data,N,K,D,100)
均值:(5, 13),协方差:(5, 13, 13),权值(5, 1)
GMM训练,EM算法
1)E步 O(样本数*高斯数)
In [7]:
1
2
3
4
5
6
def e_step(): # O(样本数*高斯数)
num = np.zeros((K,1))
for n in range(N):
for k in range(K):
num[k] = pi_k[k]* (multivariate_normal.pdf(data[n],mu_k[k],cov_k[k],allow_singular=True))
z_n_k[n] = np.reshape(num/np.sum(num),(K,))
2)M步 O(样本数*高斯数)
In [8]:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def special_op(array_1,array_2,N):
for n in range(N):
array_1[:,n] *= array_2[n]
return array_1
def m_step():
n_k = np.sum(z_n_k,axis = 0)
#print("--->",n_k)
# 更新均值 O(高斯数*样本数)
for i in range(K):
temp = np.zeros((1,D))
for n in range(N):
temp += z_n_k[n][i]*data[n,:]
mu_k[i] = (1/n_k[i])*temp
#print("--mu",mu_k)
# 更新协方差 O(高斯数*样本数)
for i in range(K):
cov_k[i] = np.dot(special_op((data - mu_k[i,:]).T,(z_n_k[:,i]),N), (data-mu_k[i])) / n_k[i]
cov_k[i] = cov_k[i] + 0.001*np.eye(cov_k[i].shape[0])
#print("--cov",cov_k)
# 更新权值 O(高斯数)
for i in range(K):
pi_k[i] = n_k[i]/N
#print("--pi",pi_k)
3)计算对数似然值
In [9]:
1
2
3
4
5
6
7
8
def calculate_likelihood():
log_likelihood = 0
for n in range(N):
temp = 0
for k in range(K):
temp += pi_k[k] * (multivariate_normal.pdf(data[n],mu_k[k],cov_k[k],allow_singular=True))
log_likelihood += np.log(temp)
return log_likelihood
训练 O(样本数 * 高斯数 * 迭代次数)
In [10]:
1
2
3
4
5
6
7
8
9
10
11
12
13
iterations = 0
old_likelihood = 0
new_likelihood = 9999
likelihood = []
while(abs(old_likelihood - new_likelihood)>1 and iterations < 300):
iterations += 1
old_likelihood = new_likelihood
e_step()
m_step()
new_likelihood = calculate_likelihood()
likelihood.append(new_likelihood)
print("iterations:{0}|likelihood:{1}|==>{2}".format(str(iterations),str(new_likelihood),abs(old_likelihood - new_likelihood)))
| iterations:1 | likelihood:[-41727.69566344] | ==>[51726.69566344] |
| iterations:2 | likelihood:[-41657.79378562] | ==>[69.90187781] |
| iterations:3 | likelihood:[-41624.9806361] | ==>[32.81314952] |
| iterations:4 | likelihood:[-41600.29602432] | ==>[24.68461177] |
| iterations:5 | likelihood:[-41579.64113783] | ==>[20.65488649] |
| iterations:6 | likelihood:[-41566.09712261] | ==>[13.54401522] |
| iterations:7 | likelihood:[-41553.62265376] | ==>[12.47446885] |
| iterations:8 | likelihood:[-41536.2774766] | ==>[17.34517717] |
| iterations:9 | likelihood:[-41517.26574647] | ==>[19.01173013] |
| iterations:10 | likelihood:[-41500.14429818] | ==>[17.12144829] |
| iterations:11 | likelihood:[-41489.03003217] | ==>[11.11426601] |
| iterations:12 | likelihood:[-41480.68690576] | ==>[8.34312641] |
| iterations:13 | likelihood:[-41470.33603076] | ==>[10.350875] |
| iterations:14 | likelihood:[-41453.93115919] | ==>[16.40487158] |
| iterations:15 | likelihood:[-41442.26626295] | ==>[11.66489623] |
| iterations:16 | likelihood:[-41434.55955465] | ==>[7.7067083] |
| iterations:17 | likelihood:[-41429.09534935] | ==>[5.4642053] |
| iterations:18 | likelihood:[-41426.09470219] | ==>[3.00064717] |
| iterations:19 | likelihood:[-41424.56705551] | ==>[1.52764668] |
| iterations:20 | likelihood:[-41423.31758667] | ==>[1.24946884] |
| iterations:21 | likelihood:[-41422.0260741] | ==>[1.29151256] |
| iterations:22 | likelihood:[-41420.80580901] | ==>[1.22026509] |
| iterations:23 | likelihood:[-41419.63721214] | ==>[1.16859687] |
| iterations:24 | likelihood:[-41418.57098572] | ==>[1.06622643] |
| iterations:25 | likelihood:[-41417.88242551] | ==>[0.68856021] |
存UBM模型
In [11]:
1
2
final_dict = {"mean":mu_k,"cov":cov_k,"pi":pi_k,"likelihood":likelihood}
np.save("ubm_file_name",final_dict)
In [12]:
1
2
3
4
5
6
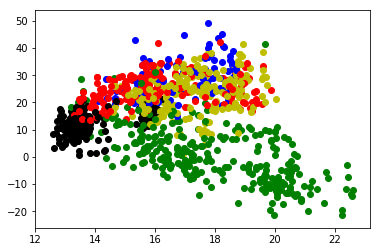
def plot(z_n_k):
plt.figure()
color_array = ["r","g","b","y","black"]
for i,each in enumerate(data):
plt.scatter(each[0],each[1],c = color_array[np.argmax(z_n_k[i,:])],edgecolor = color_array[np.argmax(z_n_k[i,:])])
plt.show()
In [13]:
1
plot(z_n_k)
MAP 实验
In [1]:
1
2
3
import numpy as np
import csv
from scipy.stats import multivariate_normal
定义变量
In [2]:
1
2
3
4
5
6
7
8
9
10
11
N = 1000
D = 13
K = 5
z_n_k = np.zeros((N,K))
mu_k = np.zeros((K,D))
mu_new = np.zeros((K,D))
n_k = np.zeros((K,1))
pi_k = np.zeros((K,1))
cov_k = np.zeros((K,D,D))
data = np.zeros((N,D))
读取 UBM 模型
In [3]:
1
2
3
4
ubm = np.load("ubm_file_name.npy").item()
mu_k = ubm["mean"]
cov_k = ubm["cov"]
pi_k = ubm["pi"]
读取注册人的MFCC数据
In [4]:
1
2
3
4
5
6
7
with open("data/english1.csv") as f_data:
reader_data = csv.reader(f_data)
for i,each_data in enumerate(reader_data):
if i == N:
break
data[i,:] = list(map(float,each_data))
data.shape
Out[4]:
1
(1000, 13)
MAP变量
In [5]:
1
2
3
4
5
old_likelihood = 99999
new_likelihood = 0
likelihood_list = []
iterations = 0
final_dict = {}
MAP自适应
In [6]:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
while(abs(old_likelihood - new_likelihood) > 1e-4 and iterations < 300):
iterations += 1
old_likelihood = new_likelihood
print("epoch:",iterations)
# 第一步:E步
num = np.zeros((K,1))
for n in range(N):
for k in range(K):
num[k] = pi_k[k] * (multivariate_normal.pdf(data[n],mu_k[k],cov_k[k]))
z_n_k[n] = np.reshape(num/np.sum(num),(K,))
print("finished E step...")
n_k = np.sum(z_n_k,axis = 0)
n_k += 1e-10
for i in range(K):
temp = np.zeros((1,D))
for n in range(N):
temp += z_n_k[n][i]*data[n,:]
mu_new[i] = (1/n_k[i])*temp
# 第二步:MAP
# 1.计算修正因子
adaptation_coefficient = n_k/(n_k + 16.0)
# 2.更新均值
print("beginning adaptation...")
for k in range(K):
mu_k[k] = (adaptation_coefficient[k] * mu_new[k]) + ((1 - adaptation_coefficient[k]) * mu_k[k])
# 计算对数似然值
log_likelihood = 0
print("calculating likelihood")
for n in range(N):
temp = 0
for k in range(K):
temp += pi_k[k] * (multivariate_normal.pdf(data[n],mu_k[k],cov_k[k]))
log_likelihood += np.log(temp)
new_likelihood = log_likelihood
likelihood_list.append(log_likelihood)
print(abs(old_likelihood - new_likelihood))
print("************************")
epoch: 1
finished E step…
beginning adaptation…
calculating likelihood
[41417.85159291]
********
epoch: 2
finished E step…
beginning adaptation…
calculating likelihood
[0.00215444]
********
epoch: 3
finished E step…
beginning adaptation…
calculating likelihood
[0.00017987]
********
epoch: 4
finished E step…
beginning adaptation…
calculating likelihood
[1.62435317e-05]
********
存MAP
In [7]:
1
2
final_dict = {"mean":mu_k,"cov":cov_k,"pi":pi_k,"likelihood":np.array(likelihood_list)}
np.save('map_file_name',final_dict)
GMM-UBM 实验
In [1]:
1
2
3
4
5
6
7
import numpy as np
import python_speech_features as psf
from scipy.io import wavfile
from IPython.lib.display import Audio
import matplotlib.pyplot as plt
import pandas as pd
import time
读取wav
In [2]:
1
2
3
4
5
6
NO_SPEAKERS = 4 # 说话人个数
'''读取wav'''
spk = [wavfile.read('data/english' + str(i) + '.wav') for i in range(1, NO_SPEAKERS + 1)]
for i in range(NO_SPEAKERS):
print("说话人 "+ str(i+1) + " 注册时长约为" + str(round(len(spk[i][1])/spk[i][0],2)))
说话人 1 注册时长约为21.87
说话人 2 注册时长约为21.08
说话人 3 注册时长约为19.72
说话人 4 注册时长约为35.97
In [3]:
1
Audio(spk[0][1], rate=spk[0][0])
Out[3]:
Your browser does not support the audio element.
In [4]:
1
2
3
4
5
6
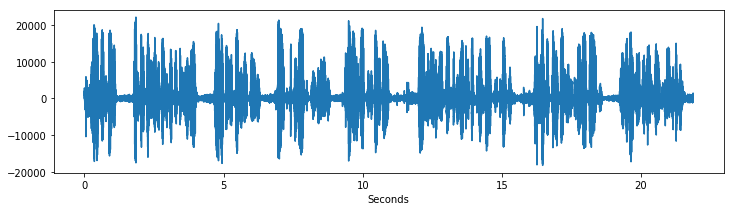
samples = spk[0][1]
sample_rate = spk[0][0]
plt.figure(figsize=(12, 3))
plt.plot(np.arange(0, len(samples))/sample_rate, samples)
plt.xlabel("Seconds")
plt.show()
提取MFCC特征(没有进行VAD)
In [5]:
1
2
3
4
spk_mfcc = [psf.mfcc(spk[i][1]) for i in range(NO_SPEAKERS)]
print("MFCC的维度:" + str(spk_mfcc[1].shape[1]))
for i in range(NO_SPEAKERS):
print("说话人 "+ str(i+1) + " 帧数为" + str(len(spk_mfcc[i])))
MFCC的维度:13
说话人 1 帧数为6027
说话人 2 帧数为5809
说话人 3 帧数为5434
说话人 4 帧数为9914
MFCC特征去均值
In [6]:
1
2
3
for i, speaker_mfcc in enumerate(spk_mfcc):
average = sum(speaker_mfcc) / len(speaker_mfcc)
spk_mfcc[i] -= average
构造数据集
1
2
3
4
5
6
7
8
9
10
11
12
In [7]:
data = []
lable = []
for i in range(NO_SPEAKERS):
data.extend(spk_mfcc[i])
lable.extend([i] * len(spk_mfcc[i]))
data = np.array(data)
lable = np.array(lable)
totals = pd.DataFrame(data)
totals['ID'] = lable
totals.head()
Out[7]:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ID | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.371644 | 1.270565 | -10.592120 | 6.482770 | 0.604627 | 1.983192 | 1.155763 | -5.674416 | -8.051335 | -4.330449 | 8.076310 | 12.182103 | 4.984159 | 0 |
| 1 | -0.557781 | -0.455990 | -4.431377 | -3.883203 | 2.685134 | 3.075300 | -0.623503 | 1.753843 | -7.239031 | 2.268565 | 22.521281 | 3.943048 | 6.346416 | 0 |
| 2 | -0.513799 | 0.334581 | -0.451569 | 1.178010 | -0.084850 | 7.185073 | -5.492316 | -4.490118 | -7.867695 | -4.077515 | 11.248673 | -1.346506 | 2.689593 | 0 |
| 3 | 0.134963 | 6.321659 | -12.745849 | 8.427790 | -5.006953 | -1.993289 | 2.605190 | -10.303228 | 6.116971 | 3.338217 | -2.754081 | 9.966781 | -1.586174 | 0 |
| 4 | 0.486162 | 12.087440 | -21.794999 | 19.800708 | -13.445799 | -0.883039 | -6.476362 | -11.099748 | 4.658329 | 6.499434 | -8.429618 | 16.611682 | -4.249450 | 0 |
构造训练集
In [8]:
1
2
3
4
5
6
7
8
9
train_size = 0.9 #训练集大小
spk_train_size = []
# lable = [] # 还可以加label
for i in range(NO_SPEAKERS):
spk_train_size.append(int(train_size * len(spk_mfcc[i])))
print("每个说话人的训练集大小(帧数):", end=" ")
print(spk_train_size)
每个说话人的训练集大小(帧数): [5424, 5228, 4890, 8922]
构造背景语料
In [9]:
1
2
3
4
5
6
7
8
9
10
11
12
13
total_mfcc = [] # 总的背景语料
spk_start = [] # 每个说话人语料的开始
spk_end = [] # 每个说话人语料的结束
for i in range(NO_SPEAKERS):
spk_start.append(len(total_mfcc))
total_mfcc.extend(spk_mfcc[i][:spk_train_size[i]])
spk_end.append(len(total_mfcc))
print("背景语料总帧数:" + str(len(total_mfcc)))
print("start:", end=" ")
print(spk_start)
print("e n d:", end=" ")
print(spk_end)
背景语料总帧数:24464 start: [0, 5424, 10652, 15542] e n d: [5424, 10652, 15542, 24464]
训练模型
In [10]:
1
2
3
4
5
6
7
from sklearn.mixture import GaussianMixture
GMM = []
UBM = []
# 每一个人训练一个GMM 和 一个 UBM
for i in range(NO_SPEAKERS):
GMM.append(GaussianMixture(n_components= 32, covariance_type= 'diag'))
UBM.append(GaussianMixture(n_components= 32, covariance_type= 'diag'))
In [11]:
1
2
3
4
5
6
7
8
9
10
11
12
for i in range(NO_SPEAKERS):
print(str(i+1) + "-GMM开始", end=",")
start = time.time()
GMM[i].fit(spk_mfcc[i][:spk_train_size[i]])
end = time.time()
print("耗时: {}s ".format(round(end-start,2)), end="--> ")
print(str(i+1) + "-UBM开始", end=",")
start = time.time()
UBM[i].fit(total_mfcc[:spk_start[i]] + total_mfcc[spk_end[i]:])
end = time.time()
print("耗时: {}s ".format(round(end-start,2)), end="--> ")
print()
1-GMM开始,耗时: 0.56s –> 1-UBM开始,耗时: 2.73s –>
2-GMM开始,耗时: 0.52s –> 2-UBM开始,耗时: 1.85s –>
3-GMM开始,耗时: 0.53s –> 3-UBM开始,耗时: 2.72s –>
4-GMM开始,耗时: 0.87s –> 4-UBM开始,耗时: 2.01s –>
预测,评估
In [12]:
1
2
3
4
5
6
7
8
9
10
11
for i in range(NO_SPEAKERS):
print("说话人:{}".format(i+1))
# 似然比检验
x = GMM[i].score_samples(spk_mfcc[i][spk_train_size[i] + 2 : ]) - UBM[i].score_samples(spk_mfcc[i][spk_train_size[i] + 2 : ])
total = 0
correct = 0
for i in x:
if i > 0:
correct +=1
total += 1
print("准确率(属于GMM的帧/总帧数) is {}".format(correct/total))
说话人:1
准确率(属于GMM的帧/总帧数) is 0.8585690515806988
说话人:2
准确率(属于GMM的帧/总帧数) is 0.4421416234887737
说话人:3
准确率(属于GMM的帧/总帧数) is 0.5940959409594095
说话人:4
准确率(属于GMM的帧/总帧数) is 0.7525252525252525
In [13]:
1
2
3
4
5
6
7
8
confusion = np.zeros((NO_SPEAKERS,NO_SPEAKERS),dtype=int)
for i in range(NO_SPEAKERS):
for j in range(NO_SPEAKERS):
x = GMM[j].score_samples(spk_mfcc[i][spk_train_size[i] + 2:]) -
UBM[j].score_samples(spk_mfcc[i][spk_train_size[i] + 2:])
for score in x:
if score > 0:
confusion[i][j] += 1
In [14]:
1
2
3
4
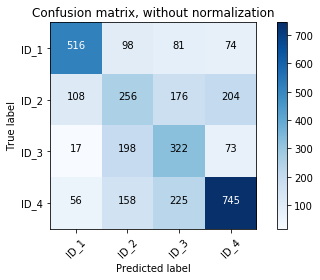
class_names = ["ID_1","ID_2","ID_3","ID_4"]
from confusion_plt import plot_confusion_matrix
plot_confusion_matrix(confusion, classes=class_names,
title='Confusion matrix, without normalization')
Confusion matrix, without normalization
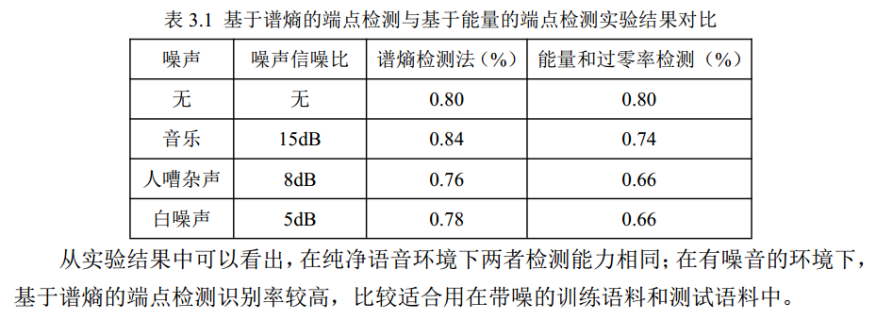
附录:一些论文实验结果的参考
端点检测对有噪声数据的影响
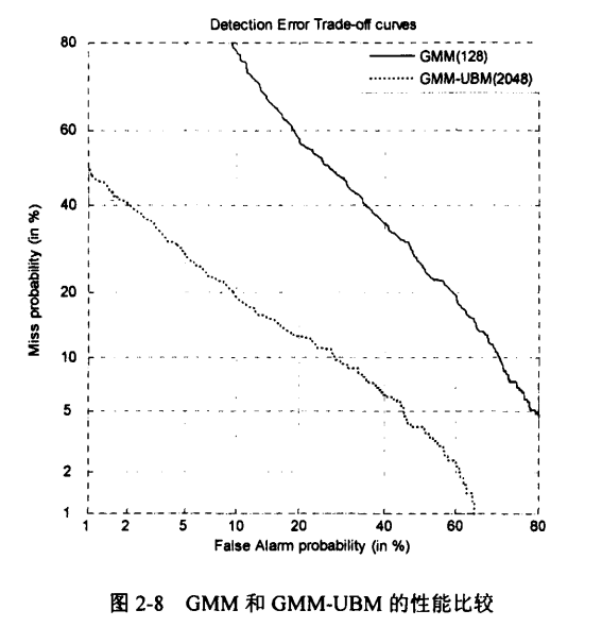
UBM-GMM与GMM模型对比
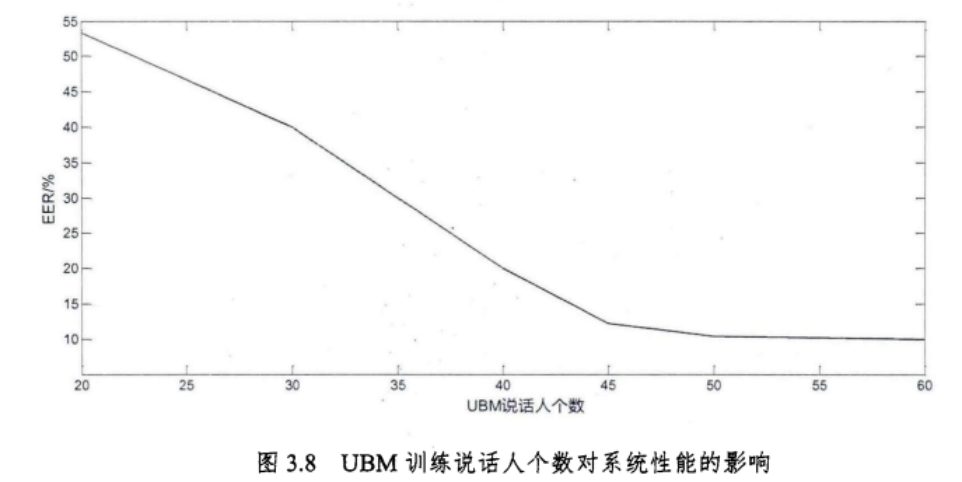
UBM训练人数对模型的影响
测试语音长度对模型的影响
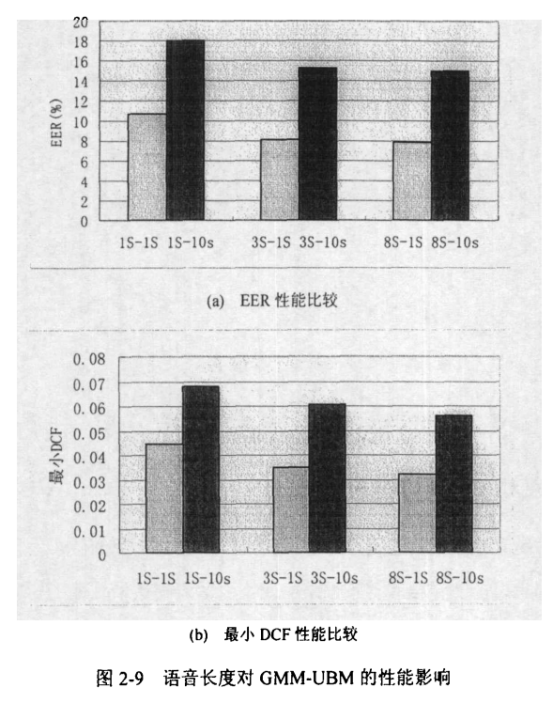
MFCC特征数对EER的影响

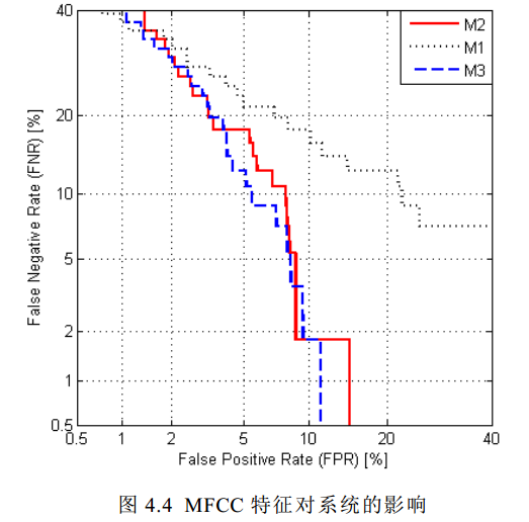
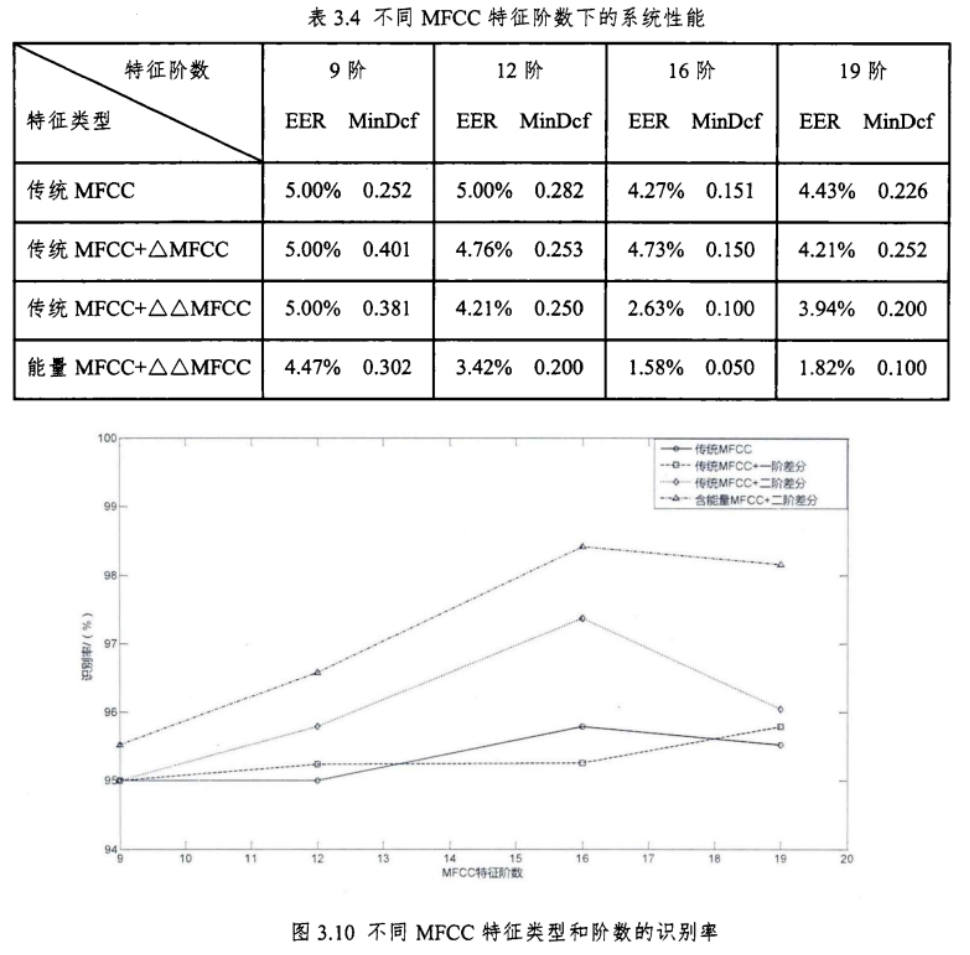
高斯数对EER的影响

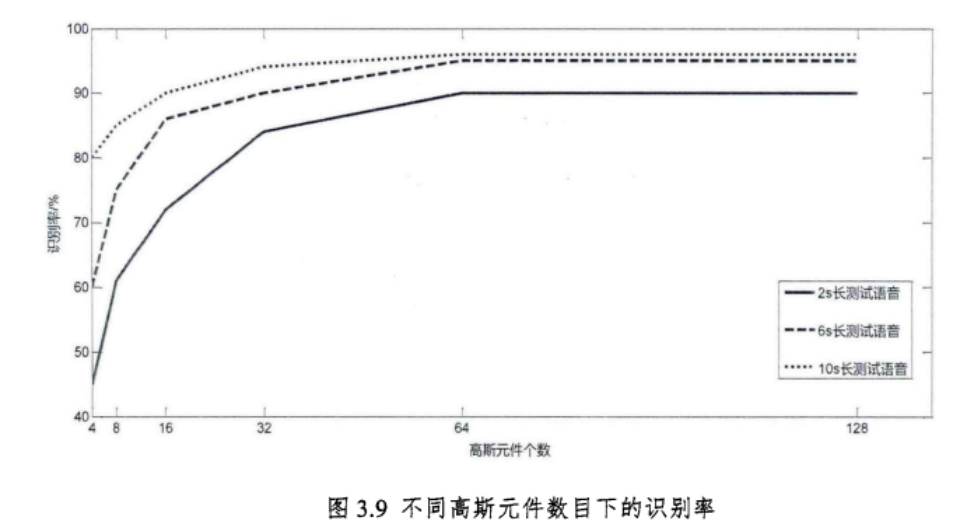
i-vector和UBM对比
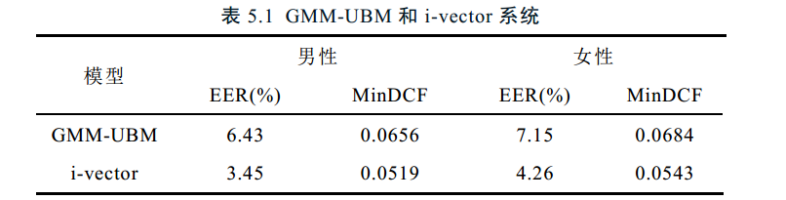
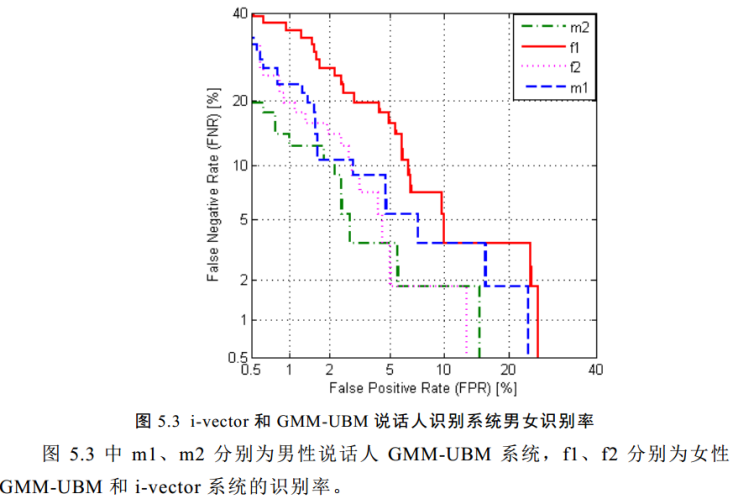
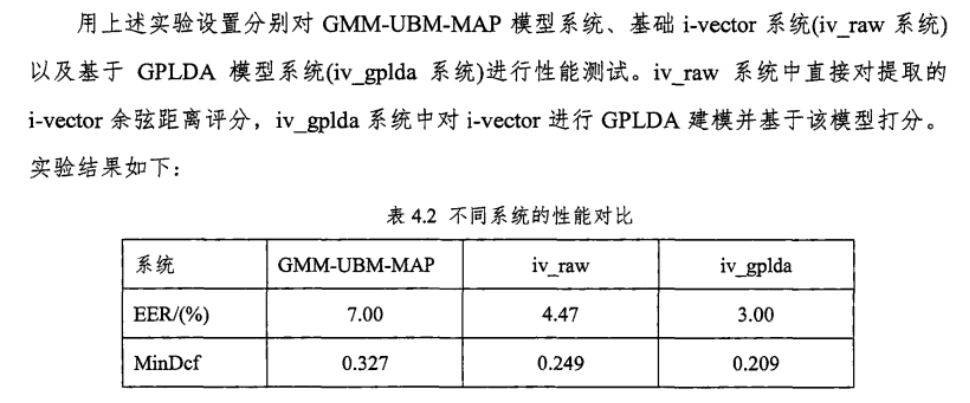
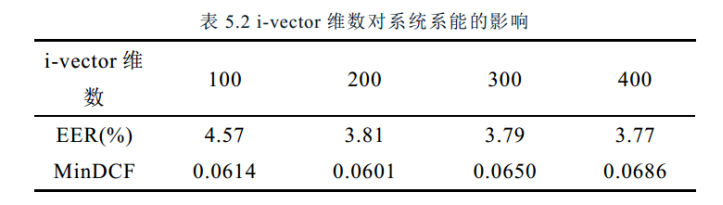
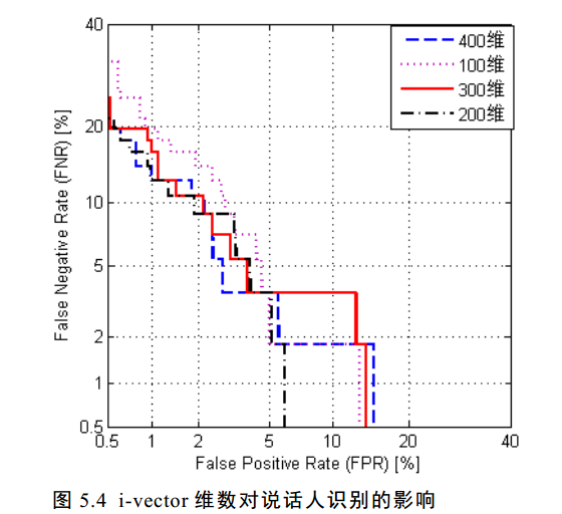
i-vector维度对模型的影响