Title: Ibiebe Alphabets and Idiograms
Creator: Bruce Onobrakpeya
Creator Nationality: Nigerian
Creator Gender: Male
Creator Birth Place: Agbarha-Otor
Date Created: 1982
Location Created: Nigeria
Physical Dimensions: 134 x 106cm
Type: Etching
Original Source: Yemisi Shyllon Museum of Art
Rights: Yemisi Shyllon Museum of Art, Pan-Atlantic University
Medium: Metal Foil Etching
《图解密码技术》,这本书个人觉得是很好的基础入门书籍,生动形象的阐述密码学的基本框架和部分技术细节。本篇主要讲解非对称密钥RSA和混合密码
公钥密码
公钥加密,私钥解密
密钥配送问题
如何安全的在通信双方进行密钥的配送
预先共享密钥
就是预先通过安全的途径(比如物理途径,亲自交到手上)将密钥交给对方
存在的问题:
1)安全的途径,如何保证?
2)人越多,数量越大,难以管理(1000个人之见互相通信,需要 1000*999/2=499500 个密钥)
密钥分配中心
Key Distribution Center(KDC),密钥分配中心
在进行通信前,KDC会生成一个通信密钥,每个人从KDC那里获取到共享密钥即可
简要过程:
1)KDC保存所有人的密钥
2)A\B 需要通信时,KDC生成一个随机密钥作为通信密钥
3)用A\B的密钥分配加密这个随机通信密钥,发送给A\B
4)A\B 分别用自己的密钥进行解密,得到通信密钥
存在的问题:
1)KDC 的安全,被入侵则所有人的密钥都会被盗
2)KDC 的稳定性,宕机则所有人无法正常通信
Diffie Hellman 密钥协商
DH 密钥协商算法的核心:有限域的离散对数问题
已知: $ G, P, G^A \mod P, $ 无法在有效的时间内计算出 A 的值
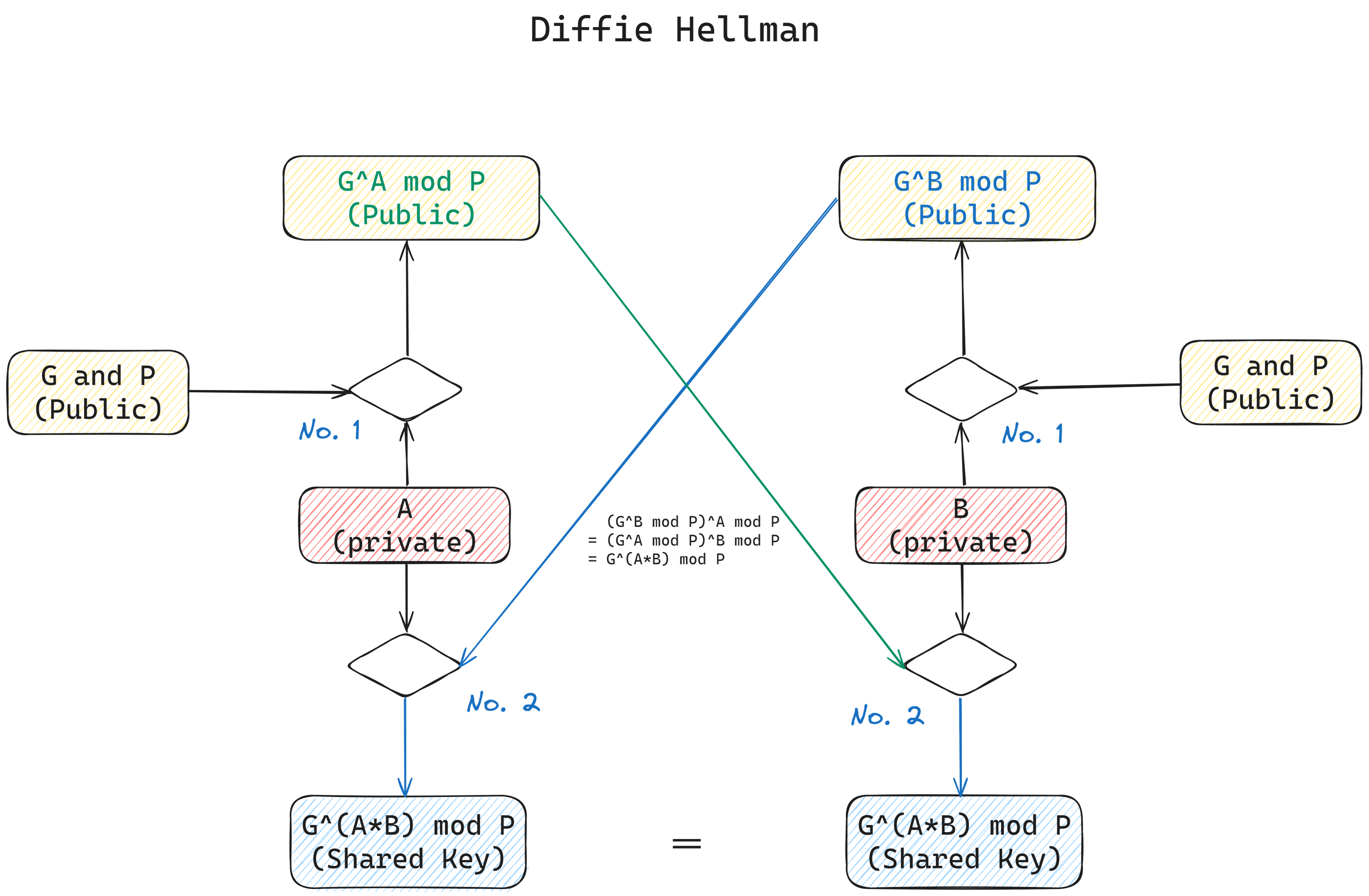
其中:
1)P 是一个大质数,G 是 P 的一个生成元
2)A 和 B 都是 1 ~ P-2 之间的整数,值要严格保密
3)生成的共享密钥为: $ G^{A*B} \mod P $
公钥密码
这里有两种方式:
1)直接使用公钥对信息进行加密,接收者使用私钥进行信息解密,从而实现加密通信。如果中途信息被窃取,攻击者也没法解密,因为没有私钥解密
2)因为公钥密码的加解密过程复杂,效率较低,所以一般不直接作为加密通信的密钥。因为可以使用公钥密码系统对共享通信密钥加密传输,再使用共享密钥进行信息通信
模运算
mod,模运算,除法求余数的运算
-
减法是加法的逆运算
-
除法是乘法的逆运算
-
对数是乘方的逆运算
模运算中的对数称为离散对数
几个性质(交换律,结合律)用一个式子表示:
$7^{16} \mod 12$
$= (7^4 * 7^4 * 7^4 * 7^4) \mod 12$
$= [(7^4 \mod 12) * (7^4 \mod 12) * (7^4 \mod 12) * (7^4 \mod 12)] \mod 12$
$= {[(7^2 \mod 12) * (7^2 \mod 12)] \mod 12 *…} \mod 12 $
$= {[(49 \mod 12) * (49 \mod 12)] * …} \mod 12 $
$= (1 * 1 * …) \mod 12$
$= 1 \mod 12$
$= 1$
RSA
加密:
$
密文 = 明文^E \mod N
$
{E, N}即为加密密钥,公钥
解密:
$
明文 = 密文^D \mod N
$
{D, N}即为解密密钥,私钥
所以RSA加解密过程都很简单:明文的E次方除以N的余数即为密文,密文的D次方除以N的余数即为明文
难度在于,N、E、D必须满足一定的条件:
-
N = p * q(p、q互为大质数)
-
E、D 互为 mod L 的质数,即 (E * D) mod L = 1
-
L = (p-1, q-1) 的最小公倍数,业界一般取L为n的欧拉函数:L=(q-1)·(p-1)
这里用一个简单的例子来展示过程
生成密钥
1)随机选取两个质数p、q(大质数计算起来太过复杂,这里就用小质数代替),计算 N
1
2
3
4
p = 17
q = 19
N = p * q = 17 * 19 = 323
N 的长度就是密钥长度。323的二进制 101000011 是9位,所以这个密钥就是9位
实际应用中,RSA密钥一般是1024位,重要场合则为2048位
2)计算L,这里使用欧拉函数取 L = φ(n) = (q-1)(p-1)
1
L = (q-1) * (p-1) = 16 * 18 = 288
3)随机选择一个整数E,要求 1 < E < L,且E与φ(n)互质
这里在 1~288 之间选择 11(实际情况中,一般选择 65537)
4)计算D,D为E对于L的模反元素,即E*D能被L除后余1
1
2
3
(E * D) mod L = 1
=> E * D - 1 = n*L
=> 11D - 1 = 288n
即为求解 11x + 288y = 1 的二元一次方程的一个整数解
这里可以使用扩展欧几里得算法计算出:
1
2
x = 131
y = -5
因此,求得 D为131
5)最终得出密钥
1
2
加密密钥(公钥)为: (E, N) = (11, 323)
解密密钥(私钥)为: (D, N) = (131, 323)
安全性
在整个过程中,使用到了:
1
p, q, N, L, D, E
其中,公开的是公钥 (E, N),需要保密的是私钥(D, N),所以最重要的是不能通过E和N,推导出D
通过第四步可知,计算D需要知道E和L,E已知,L则是q和p计算得到,而N=q*p,那么能不能通过N进行因数分解得到p和q呢?
不能,因为大整数的因数分解,目前暂时没有合适的算法,只有暴力破解,所以只要大整数足够大,那么就是安全的
这就是RSA算法基于的安全假设:大整数的因数分解难题
小结:对称密码通过将明文转换为复杂的形式来保证机密性,非对称密码则是基于数学上困难的问题来保证机密性
加密
前文已经说过,加密的过程是: $ 密文 = 明文^E \mod N $
这里,明文必须是小于N的整数(编码转换成整数,小于N是因为后面要对N取模,如果大于N,则解密时无法正确还原)
假设明文时 21,此时公钥为(E, N) = (11, 323)
计算得:
1
密文 = 21^11 mod 323 = 319
解密
解密的过程是: $ 明文 = 密文^D \mod N $
上一步中,得到密文319,私钥为(D, N) = (131, 323)
计算得:
1
明文 = 319^131 mod 323 = 21
与我们上面假设的明文21能够对应上,因此完美的进行了加解密操作
正确性证明
参考RSA维基百科
首选取两个互质数$p$和$q$, 乘法计算$p * q$得到$N$。
然后计算出欧拉$\Phi (N)$($p$和$q$都是质数):
$
\Phi (N) = (p - 1)(q - 1)
$
这时候我们随机选择一个整数$e$,条件是$1 < e < \Phi(N)$,且$e$与$\Phi(N)$ 互质
接着我们计算$e$对$\Phi(N)$的模逆元得到$d$:
$ e _d \equiv 1(mod \Phi(N)) $
这个公式简单的说就是 $e_ d$除以$\Phi(N)$得到的余数为1,这个公式可以转换成
$ ed \ \%\ ((p - 1) (q - 1)) = 1 $
即:$ ed = k(p-1)(q-1)+1 $
于是,RSA公钥为$(N,e)$,私钥为$(N,d)$
加密原文$m$得到密文
$ x = m^{e} \% N $
解密公式为
$ m = x^{d} \% N $
证明解密逻辑
在 $ m<N $ 的狀況下证明$ m = x^{d} \% N $,就是证明$ x^{d} \% N - m = 0 $
$ x^{d}\% N-m $
$ =(m^{e}\%N)^{d}\%N-m $
$ =m^{ed}\%N-m \quad \because a ^ b \% p = ((a \% p)^b) \% p $
$ =m^{k(p-1)(q-1)+1}\%N-m $
$ =m*(m^{k(p-1)(q-1)}-1)\%N $
当m与N互质时,根据费马小定理公式
$ a^{p-1} \equiv 1 (mod\ p)$
$ \Rightarrow (m^{k(q-1)})^{p-1} \equiv 1 (mod\ p)$
$ \Rightarrow (m^{k(p-1)})^{q-1} \equiv 1 (mod\ q) $
$ \Rightarrow m^{k(p-1)(q-1)} \equiv 1 (mod\ pq) $
$ \Rightarrow m^{k(p-1)(q-1)} \equiv 1 (mod\ N) $
$ \Rightarrow m*(m^{k(p-1)(q-1)}-1)\%N=0 $
当m与N不互质时,不妨设公因子为p,即$m=ph_1 (h_1<q)$
假设 q 整除 m,因此$q \mid ph_1$
因为 q 与 p 互质,根据欧几里得定理,$q \mid h_1$
所以$q \le h_1$,而这与$ h_1<q $ 矛盾,所以 q 不整除 m
此时 m 与 q 互质,根据费马小定理公式
$ a^{p-1} \equiv 1 (mod\ p)$
$ \Rightarrow m^{q-1} \equiv 1 (mod\ q)$
$ \Rightarrow m^{k(p-1)(q-1)} \equiv 1 (mod\ q)$
$ \Rightarrow m^{k(p-1)(q-1)}-1=qh_2$
$ \Rightarrow m*(m^{k(p-1)(q-1)}-1)\%N=ph_1 *qh_2\%N=Nh_1h_2\%N=0 $
证明完成!
混合密码系统
单独使用对称密码或者非对称密码各有一些问题:
-
对称密码存在密钥配送问题
-
非对称密码的处理速度远远低于非对称密码
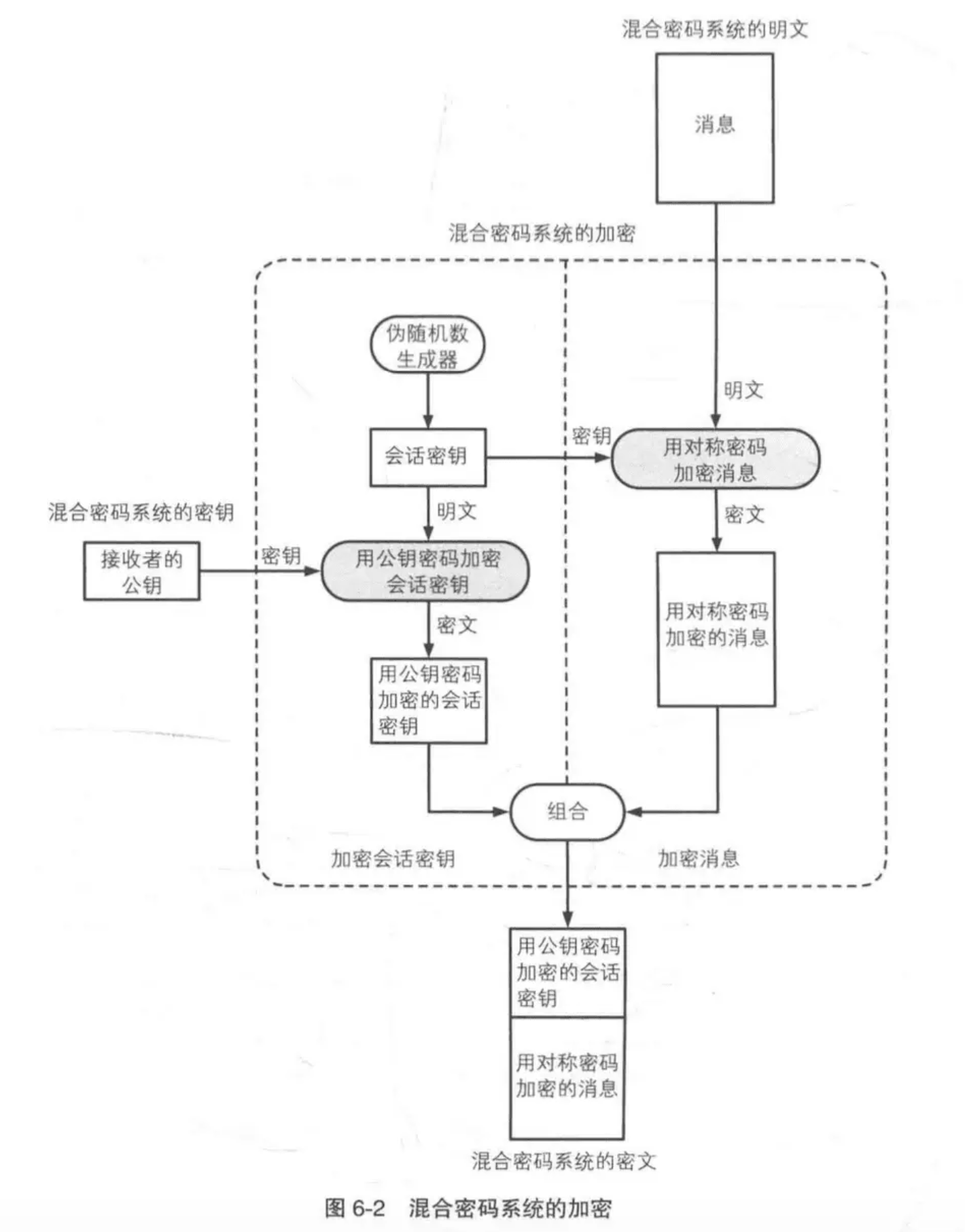
为了解决上述问题,于是就有了混合密码系统(Hybrid Cryptosystem):简单来说,就是用对称密码系统加密通信内容,用非对称密码系统加密对称密码的密钥
其加密过程大致为:
1)伪随机数生成器,生成会话秘钥(session key)
2)使用对称密码加密通信消息,此时对称密码使用的密钥是上述步骤生成的会话秘钥
3)然后使用发送者手里掌握的接收者公钥对上面的会话秘钥进行加密
4)最后,将加密后的会话秘钥和加密后的通信消息一起发送给接收者
其解密过程大致为:
1)先将加密后的会话秘钥和加密后的通信消息分离开
2)然后使用接收者手里掌握的接收者私钥对上面加密的会话秘钥进行解密获得会话秘钥
3)使用上面解密获得的会话秘钥对加密后的通信消息进行解密,获得通信信息
安全点
-
对称密码系统的密钥使用的是伪随机数生成器,要保证伪随机数生成器足够随机,不容易被暴破
-
对称密码系统本身的强度要求足够高,密钥长度确保足够长
-
非对称密码系统本身的强度要求足够高,密钥长度确保足够长
实际应用
-
PGP
-
SSL/TLS