区块链 密码学 对称密码 AES

对称加密与AES：探寻随机性的核心原理

对称加密与哈希函数的核心原理均为实现随机性，本篇主要深入探讨对称密码与AES

Posted by Yewbs on March 1, 2024

Title: Fish Magic
Creator: Paul Klee, Swiss, 1879 - 1940
Creator Nationality: Swiss
Creator Gender: Male
Creator Death Place: Muralto, Switzerland
Creator Birth Place: Münchenbuchsee, Switzerland
Date: 1925
Physical Dimensions: w38.75 x h30.39 in (Overall)
Type: Paintings
Rights: © 2014 Philadelphia Museum of Art. All rights reserved
Medium: Oil and watercolor on canvas on panel

进入web3以来，越来越感受到密码学的重要性，尤其是开始研究zkp以后，更是如此。知识，亦是常学常新，在经过了zkp的洗礼之后，重新再来看基础密码学，也有颇多新解

本篇内容主要取材于Dr Lynndell的密码学讲座，不同于图解密码系列，而是更加深入的研究对称密码和AES算法

核心原理

对称加密与哈希函数的核心原理：实现随机性

常见的实现方式主要包括三大变换：

  • 线性变换：每 bit 的输入发生变换，影响 50%输出，密文随机性高

  • 非线性变换： S-box (substitution-box)，抵抗解方程组攻击、延展攻击

  • 轮密钥加/轮常量加：添加一些随机密钥或常量，提高信息商

对称加密

统一描述

形式化描述：

初始化：双方共享一个保密随机数K ，或使用相同的设备生成一个相同的随机数K

加密：发送方使用设备生成随机数K ，对消息X ，如下计算
$ Y := K \oplus X $
发送密文Y

解密：接收方接收密文Y ，使用设备生成随机数K ，如下计算
$ X := K \oplus X $
获得消息X

AES

在前文《图解密码技术》读书笔记(1)——对称密码与分组密码中已经初步介绍过AES的概念，这里主要详解介绍下其具体的加密过程、最重要的轮函数原理以及密钥扩展的算法

AES 具体来说是一种加密标准，最终入选的具体算法是由比利时两位著名的密码学家 Joan Daemen 和 Vincent Rijmen设计的Rijndael算法

Rijndael是一个分组密码算法族，其分组长度包括128比特、160比特、192比特、224比特、256比特，密钥长度也包括这五种长度，但是最终AES只选取了分组长度为128比特，密钥长度为128比特、192比特和256比特的三个版本

下图展示了AES的算法流程：
AES

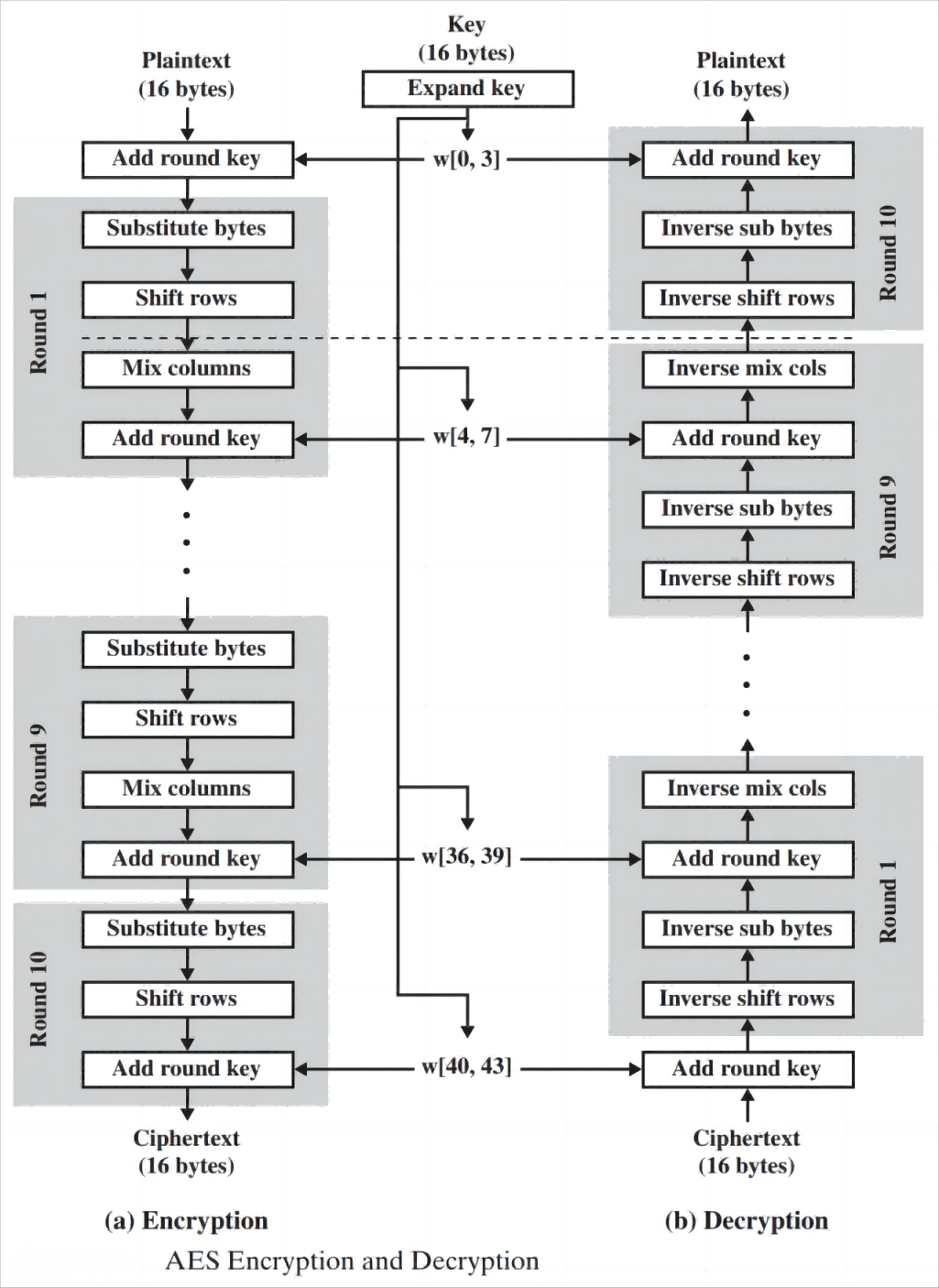
从图中可以看出，算法最关键的部分就是轮函数的运算和轮密钥的生成

轮函数

轮函数包含的4种运算操作仍然是我们开头提到的实现随机性的三大变换：

  • 线性变换：这里表现为行移位（ShiftRows）、列混淆（MixColumns）

  • 非线性变换：S-Box字节替换（SubBytes）

  • 轮密钥加（AddRoundKey）

同时，在图的右边展示的是AES解密算法的流程，可以看出解密算法的每一步分别对应加密算法的逆操作，即 加解密所有操作的顺序正好是相反的

加解密中每轮的密钥分别由种子密钥经过密钥扩展算法得到。算法中 16 字节的明文、密文和轮子密钥都以一个 4x4 的矩阵表示

下面是轮函数的详细步骤：

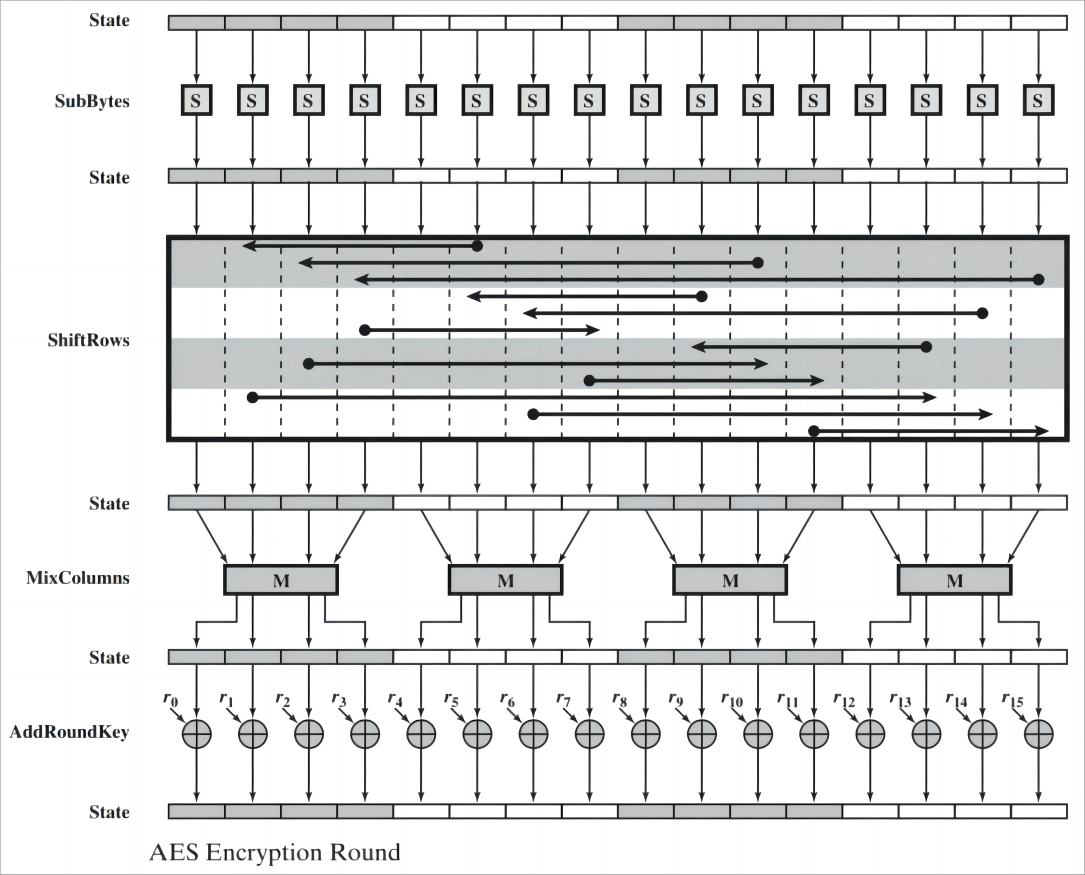
RoundFunction

字节替换 SubBytes

字节替换通过S-box完成一个字节到另一个字节的映射和替换，主要用于提供密码算法的 混淆性（非线性变换）

  • S盒变换是AES的唯一的非线性变换，是AES安全的关键

  • AES使用16个相同的S盒，DES使用的是8个不同的S盒

  • AES的S盒有8位输入，8位输出，是一种非线性置换；DES的S盒有6位输入，4位输出，是一种非线性压缩

这里直接使用一个构造好的S-box，其中a为 $S$，b为 $S ^{-1}$

S-box

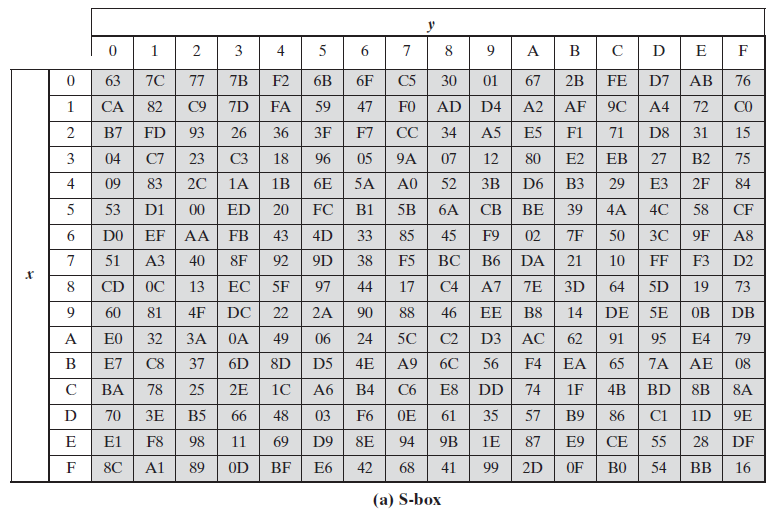
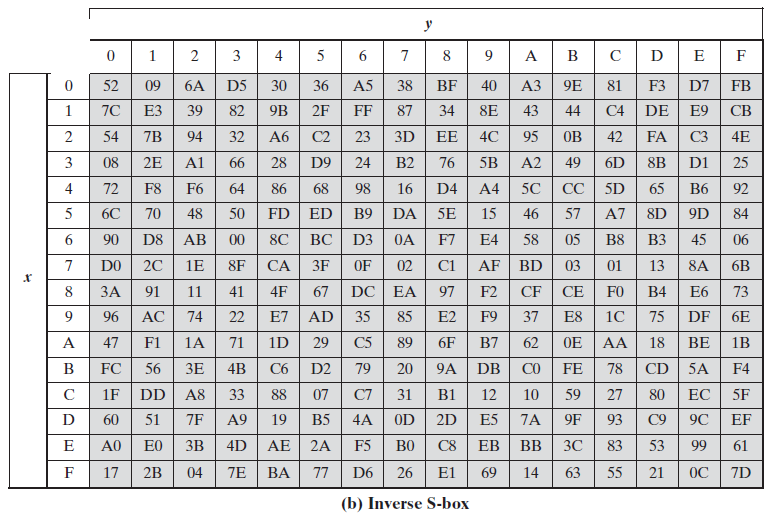
Inverse S-box

$S$ 和 $S ^{-1}$ 分别为 16X16 的矩阵，完成一个 8bit 输入到 8bit 输出的映射，输入的高 4bit 对应的值作为行标，低 4bit 对应的值作为列标

输入字节值为 a=a7a6a5a4a3a2a1a0 ，输出值为 S[a7a6a5a4][a3a2a1a0] ，$S ^{-1}$ 的变换也同理

例如：

  • 字节 00000000B 通过 $S$ 替换后的值为（S[0][0]=）63H

  • 再通过 $S ^{-1}$ 即可得到替换前的值， （S- 1 [6][3]=）00H

等价描述

  1. 按字节值的升序逐行初始化$S$盒子
    第1行是{00},{01},…,{0F}
    第2行是 {10},{11},…,{1F}
    以此类推，在 y行 x列的字节值是{yx}

  2. $S$ 盒子中每个字节映射为有限域 $GF(2^{8})$ 中的逆，其中{00}映射为{00}

  3. S 盒子中的每个字节的 8 位记为 $(b_{7},b_{6}, …, b_{0})$ ，对每个字节进行如下正变换： $ b_{i}’ = b_{i} \oplus b_{i+4mod8} \oplus b_{i+5mod8} \oplus b_{i+6mod8} \oplus b_{i+7mod8} \oplus c_{i} $
    其中$c_{i}$是值{63}字节 c 的第 i 位($c_{7}$, $c_{6}$, $c_{5}$, $c_{4}$, $c_{3}$, $c_{2}$, $c_{1}$) = (01100011)

  4. 对应的逆变换为：
    $ b_{i}’ = b_{i+2mod8} \oplus b_{i+5mod8} \oplus b_{i+7mod8} \oplus d_{i} $
    其中字节 d = {05} = 00000101

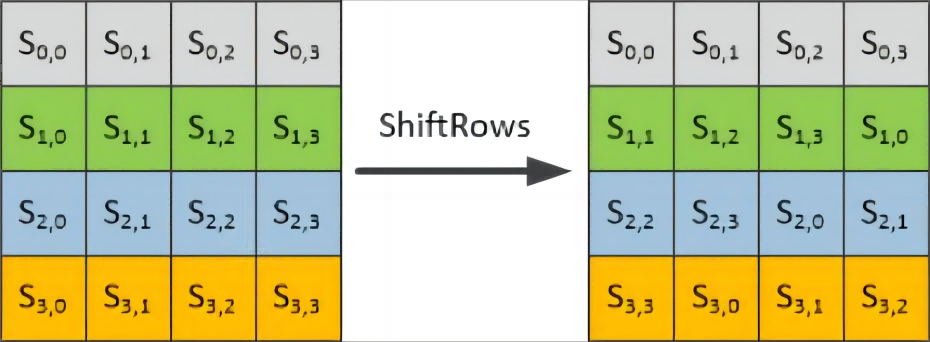
行移位 ShiftRows

行移位是一个 4X4 的矩阵内部字节之间的置换，本质在于把数据打乱重排，用于提供算法的 扩散性（线性变换）

加密中的正向行移位

ShiftRows

  • 第一行保持不变

  • 第二行循环左移 8 比特

  • 第三行循环左移 16 比特

  • 第四行循环左移 24 比特

解密中的逆向行移位

与正向行移位执行相反的操作

  • 第一行保持不变

  • 第二行循环右移 8 比特

  • 第三行循环右移 16 比特

  • 第四行循环右移 24 比特

列混淆 MixColumns

利用 $GF(2^8)$ 域上算术特性的一个代替，同样用于提供算法的 扩散性（线性变换）

加密中的正向列混淆

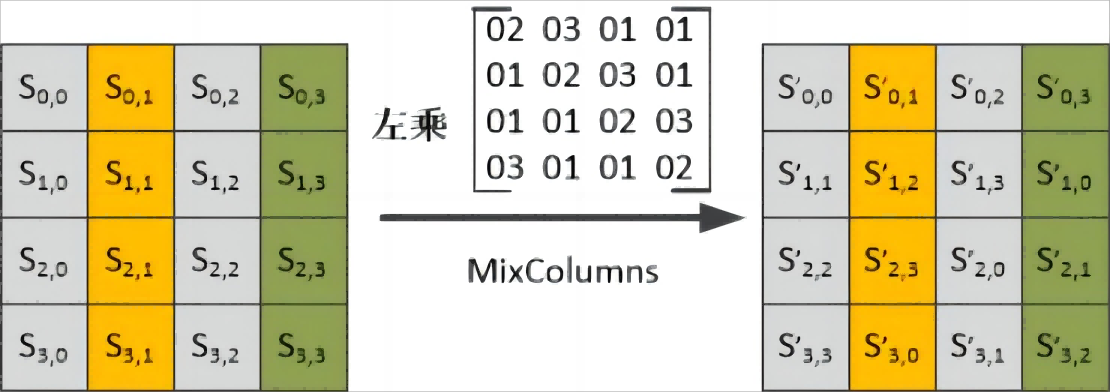
MixColumns

上述原理图中的乘法和加法都是定义在 $GF(2^8)$ 域上

可以理解为：
列混合变换把状态的列视为 $GF(2^8)$ 上的多项式 $a(x)$ 乘以一个固定的多项式 $c(x)$ ,并模一个不可约多项式 $m(x)$

不可约多项式（本原多项式），是不能写成两个次数较低的多项式之乘积的多项式，即没有因子的多项式

举个例子

假设：
$c(x)$ 为 $\lbrace C9 \rbrace$，即 $c(x) = x^{7} + x^{6} + x^{3} + 1$
$m(x) = x^{8} + x^{4} + x^{3} + x + 1$

则得到：
$ \lbrace 02 \rbrace· \lbrace C9 \rbrace \\
= (0000,0010)·(1100,1001) \\
= x · (x^{7} + x^{6} + x^{3} + 1) \mod (m(x)) \\
= x^{8} + x^{7} + x^{4} + x - (x^{8} + x^{4} + x^{3} + x + 1) \\
= x^{7} + x^{3} + 1 \\
= (1000,1001) \\
= \lbrace 89 \rbrace $

解密中的逆向列混淆

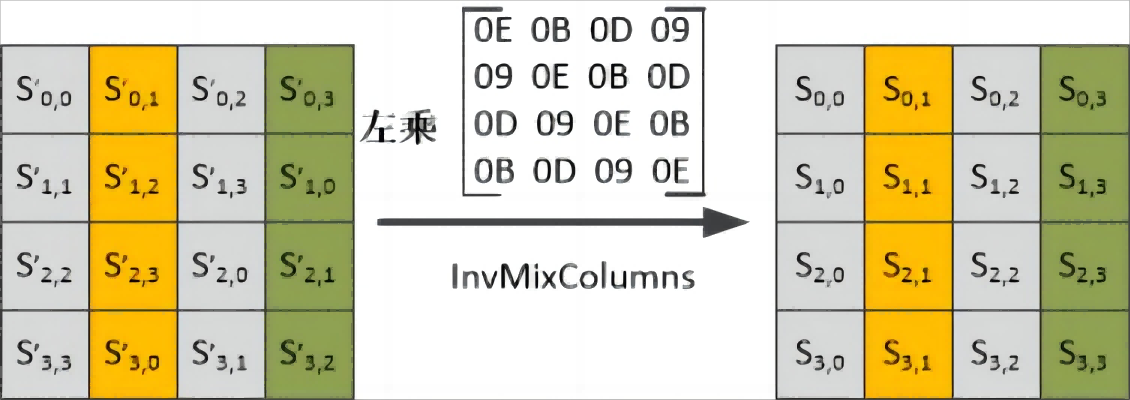
Inverse MixColumns

逆向列混淆中则是左乘正向矩阵的逆矩阵，这样就能保证逆向列混淆后恢复明文

即：

Inverse MixColumns2

在AES实现过程中，正向列混淆使用的矩阵要简单，所以 AES 加密计算复杂度更低，AES 解密计算复杂度更高
设计思想：CFB/OFB/CTR 模式仅使用 AES 加密算法，用于生成随机数来实现加密，所以需要加密矩阵的值更小，效率更高
轮密钥加 AddRoundKey

加密：每轮的输入与轮密钥异或一次，$c = m \oplus k$

解密：再异或上该轮的轮密钥即可恢复明文，$m = c \oplus k$

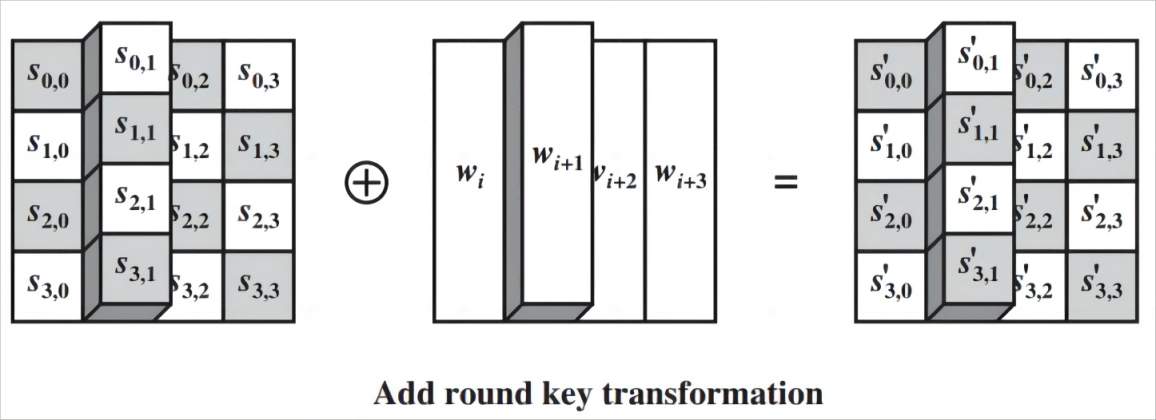
AddRoundKey

其依据的原理是“任何数和自身的异或结果为0”

这里最重要的就是轮密钥，轮密钥根据密钥扩展算法和密钥选择而产生的

密钥扩展

轮密钥在AES加解密中有着极其重要的角色

  1. 加密迭代中每一轮需要一个轮密钥参与加密

  2. 轮密钥根据密钥产生算法通过用户密钥得到

  3. 密钥产生分两步进行：

    （1）密钥扩展

    （2）轮密钥选择

  4. 密钥扩展将用户密钥扩展为一个扩展密钥

  5. 密钥选择从扩展密钥中选出轮密钥

密钥扩展算法

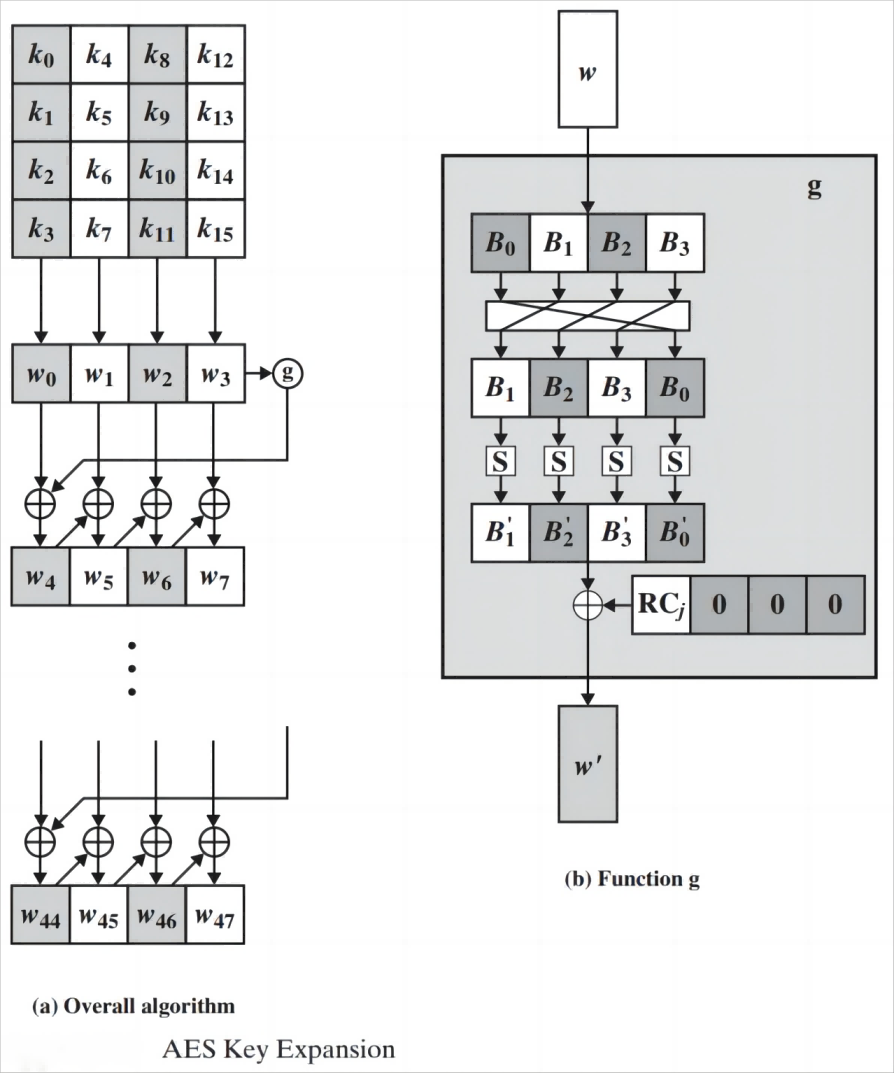
Key Expansion

比如：将 16bytes(128bit) 的密钥扩展为 43bytes(344bit)

  • 将种子密钥按图(a)的格式排列， k0、k1、...、k15 依次表示种子密钥的一个字节; 排列后用 4 个 32bit 的字表示，记为w[0]、w[1]、w[2]、w[3] 4 组，每组 4 个字节

  • 串行求解 w[j]，其中 j 是整数并且属于[4,43]

  • g 函数内部也包含了线性变换、非线性变换和轮常量加

    • 线性变换：将 w 循环左移 8bit

    • 非线性变换：分别对每个字节做 S-box 置换

    • 轮常量加：与 32bit 的常量 RC[j/4],0,0,0 进行异或， RC 是一个一维数组

举个例子

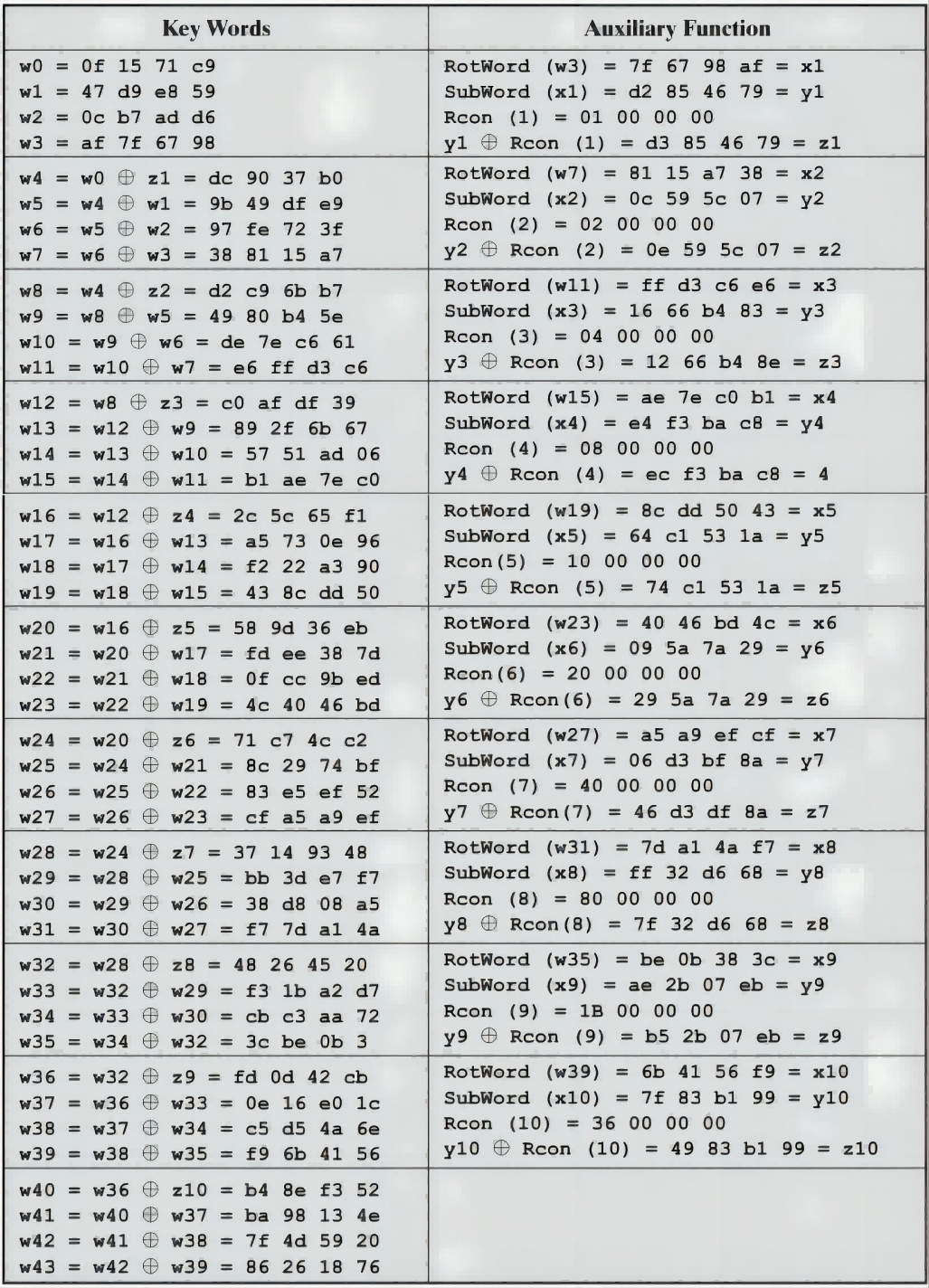
Key Expansion

轮密钥选择

根据分组大小，依次从扩展密钥中取出轮密钥

前面的Nb个字作为轮密钥0，接下来的Nb个字作为轮密钥1，以此类推…

对称加密的工作模式

Q: 分组密码每次加密 128bit 的数据，如果数据为 128bit~300Gbit 数据，应该如何加密？

A: 分组密码循环调用多次，实现对任意长数据的加密

这个循环调用的方式，就成为工作模式

常见的五种工作模式

常见的五种工作模式在《图解密码技术》读书笔记(1)——对称密码与分组密码已经简单介绍过

ECB（Electronic CodeBook），电子密码本模式

  • 能并行加密和解密
  • 如果 P1=P2 ，则 C1=C2 密文的随机性很差
  • 应用场景：仅加密 128bit 的数据

CBC（Cipher Block Chaining），密文分组链接模式

  • 随机性高
  • 传输错误则会影响后续解密正确性——雪崩效应
  • 串行加解密
  • 最后一个分组需要填充
  • 需要初始化向量
  • 应用场景：数据本地加密解密且数据量较小（或对速度无要求），则可用该方案；远程传输则不使用该方案

CFB（Cipher FeedBack），密文反馈模式

  • 需要初始化向量
  • 不能并行运算
  • 不需要填充
  • 传输错误则会影响后续解密正确性——雪崩效应
  • 每次加密 sbit，且串行，因此效率较低
  • 加密和解密过程均使用 AES 加密算法，计算效率较高

OFB（Output FeedBack），输出反馈模式

  • 需要初始化向量
  • 不能并行运算
  • 不需要填充
  • 加密和解密过程均使用 AES 加密算法，计算效率较高
  • 本质上是分组密码算法构造出流密码算法，生成任意长的随机数对消息加密

CTR（CounTeR），计数器模式

  • 用计数器代替OFB模式中的向量
  • counter1= IV，可公开传输
  • 不需要填充，独立性高， 可并行运算
  • 加密和解密过程均使用 AES 加密算法，计算效率较高
  • 本质上是分组密码算法构造流密码算法，生成任意长随机数对消息加密
  • ECIES 加密方案中，调用 AES 对称加密时，就使用了该方案

GCM模式

GCM = MAC + CTR

目前最推荐的模式，在CTR计数器模式上添加了MAC（Message Authentication Code）消息验证码

GCM 是认证加密模式，将 MAC 和 CTR计数器模式耦合，结合二者优点

  • CTR 计数器模式： 确保数据的保密性、并行性，且具有 counter=IV 可公开等优点

  • MAC：提供附加消息的完整性校验

GCM

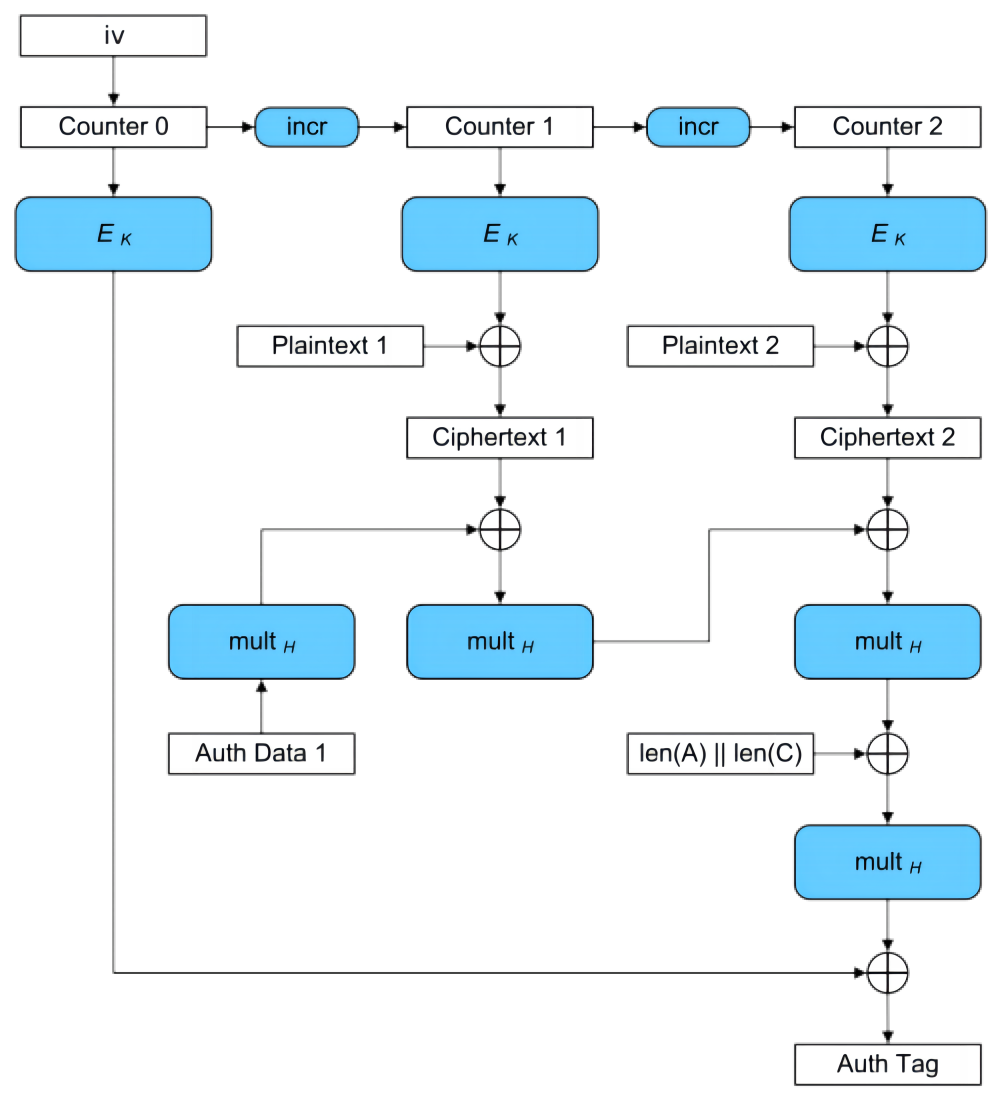
主要流程

发送方：

1）CTR 模式下，先对块进行顺序编号，然后将该块编号与初始向量(IV)组合，并使用密钥 k 对输入做 AES 加密，然后将加密的结果与明文进行 XOR 运算来生成密文

2）对于附加消息（共享秘钥），使用密钥 H(由密钥 K 得出)，运行 GMAC，将结果与密文进行 XOR 运算，生成用于验证数据完整性的身份验证标签

接收方：

密文接收者会收到一条完整的消息，包含密文、IV(计数器 CTR 的初始值)、身份验证标签(MAC 值)

接收者先使用MAC进行数据完整性校验，再进行常规的 CTR 解密过程

CATALOG
    FEATURED TAGS
    网络安全 区块链 AI安全 CTF 密码学 区块链基础 机器学习 哈希函数 ETH 声纹识别 读书笔记 对称密码 数据分析 智能合约 AES python