Title: Samson and Delilah
Creator: Anton van Dyck
Creator Lifespan: 1599/1641
Creator Nationality: flemish
Creator Gender: male
Creator Death Place: London
Creator Birth Place: Antwerp
Date Created: 1628/1630
Style: Flemish Baroque
Provenance: donated to Archduke Leopold Wilhelm
Physical Dimensions: w2540 x h1460 cm (without frame)
Inventory Number: GG 512
Type: paintings
进入web3以来,越来越感受到密码学的重要性,尤其是开始研究zkp以后,更是如此。知识,亦是常学常新,在经过了zkp的洗礼之后,重新再来看基础密码学,也有颇多新解
本篇内容主要取材于Dr Lynndell的密码学讲座,不同于图解密码系列,而是更加深入的研究Web3中比特币使用的哈希函数——SHA256
核心原理
对称加密与哈希函数的核心原理:实现随机性
常见的实现方式主要包括三大变换:
-
线性变换:每 bit 的输入发生变换,影响 50%输出,密文随机性高
-
非线性变换: S-box (substitution-box),抵抗解方程组攻击、延展攻击
-
轮密钥加/轮常量加:添加一些随机密钥或常量,提高信息商
哈希函数
哈希函数(Hash Function)是一种将任意长度的输入数据转换为固定长度输出的算法
它将输入数据经过计算和变换,生成称为哈希值(Hash Value)或哈希码(Hash Code)的固定长度字符串
哈希函数的输出长度通常是固定的,例如128位、256位或更长
关键性质:
-
单向性:已知哈希值$Y$,无法在多项式时间内计算出哈希原象$X$
-
弱抗碰撞性:已知$(X, Y)$,无法在多项式时间找到$X’$,使得$Y=Hash(X’)$
-
强抗碰撞性:攻击者无法寻找$(X, X’)$,满足$(X \neq X’)$ 且 $hash(X) == hash(X’)$
-
随机性:输出的 $Y$ 是 128bit(或256bit或更长) 的 0/1 字符串是随机的
-
可重复性:如果输入 $x1=x2$,则输出的哈希值 $Y1=Y2$
SHA256
比特币(Bitcoin)中哈希函数SHA-256主要用在下面几个方面:
挖矿:矿工通过对区块头部数据进行SHA-256哈希计算,不断尝试找到满足一定条件的哈希值,以获得比特币的奖励(Proof of Work)
区块链的完整性验证:比特币中的每个区块都包含其自身的哈希值,以及前一个区块的哈希值,通过对区块的哈希值进行计算,可以验证区块链的完整性,确保没有被篡改或修改
交易签名:在比特币交易中,SHA-256被用于计算交易数据的哈希值,以生成交易的数字签名,这样可以确保交易的完整性和真实性,防止交易数据被篡改
整体流程
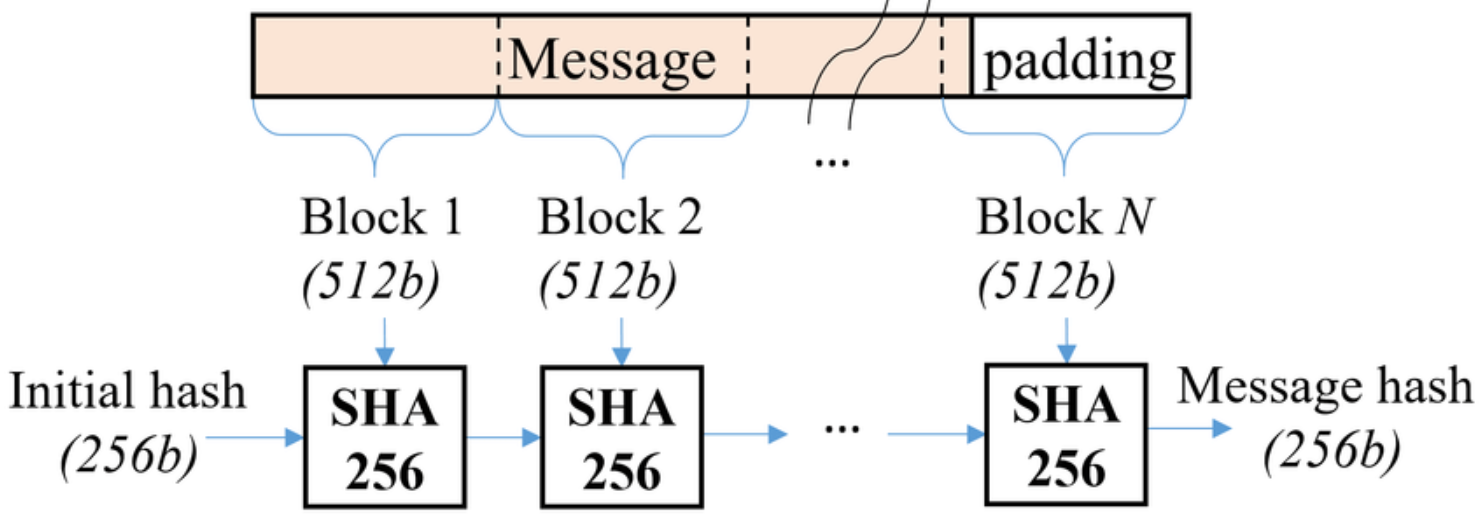
从上图可以看出,SHA256主要分为三个大步骤:初始化、对输入数据进行预处理和计算摘要
初始化
SHA256的运算过程中,需要两组基础常量:
-
其中一组为8个常量,记作$H_0$,用于后面映射函数的首次迭代
-
另一组为64个常量,记作$K_t, t \in [0, 63]$,用映射函数中的64次轮常量加
$H_0$
$H_0 = [h_0, h_1, …, h_7]$
$h_0$ = 0x6a09e667
$h_1$ = 0xbb67ae85
$h_2$ = 0x3c6ef372
$h_3$ = 0xa54ff53a
$h_4$ = 0x510e527f
$h_5$ = 0x9b05688c
$h_6$ = 0x1f83d9ab
$h_7$ = 0x5be0cd19
这8个初始向量是通过取前8个质数(2,3,5,7,11,13,17,19)的平方根的小数部分的前32位得到的
举个例子:
$ \sqrt{2} $小数部分约为 0.414213562373095048
$0.414213562373095048 = 6 \ast 16^{-1} + a \ast 16^{-2} + 0 \ast 16^{-3} + … $
所以,质数2的平方根的小数部分取前32bit就对应出了0x6a09e667
$K_t$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
K = [
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5,
0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3,
0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0xfc19dc6, 0x240ca1cc,
0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7,
0xc6e00bf3, 0xd5a79147, 0x6ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13,
0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3,
0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5,
0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208,
0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
]
与8个哈希初值类似,这些常量是对自然数中前64个质数(2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97…)的立方根的小数部分取前32bit得到的
| 选择质数的平方根(立方根)的小数部分作为初始向量可以确保初始向量的值是固定的,可以确保不同的实现和应用程序在使用SHA-256算法时得到相同的结果;同时,又具有足够的随机性,以增加哈希算法的安全性,防止哈希算法受到预计算攻击或其他类型的攻击 |
数据预处理
数据预处理主要包括数据填充和数据分解
数据填充
数据填充包括附加填充比特和附加长度两部分
填充规则:
先补第一个比特为1,然后都补 k 个0,直到长度满足对 512 取模后余数是 448,剩余 64bit 填充数据长度
-
msg,= {msg, 1, 0, …, 0, msg-len-64bit}
-
计算方法:(Len(msg)+1+k+64)/512=0 ,寻找最小自然数 k
需要注意的是,信息必须进行填充,即使长度已经满足对 512 取模后余数是 448,补位也必须要进行, 这时要填充 512 个比特
数据分解
数据分解就是将填充后的数据M 分解成 n 个大小为 512bit 的块
此后在做循环映射时,每次对 512bit 的数据块进行运算,得到的 256bit 再与下一个块进行运算,如此运行 n 次后,得到最终的哈希值,即 256bit 的数字摘要
计算摘要
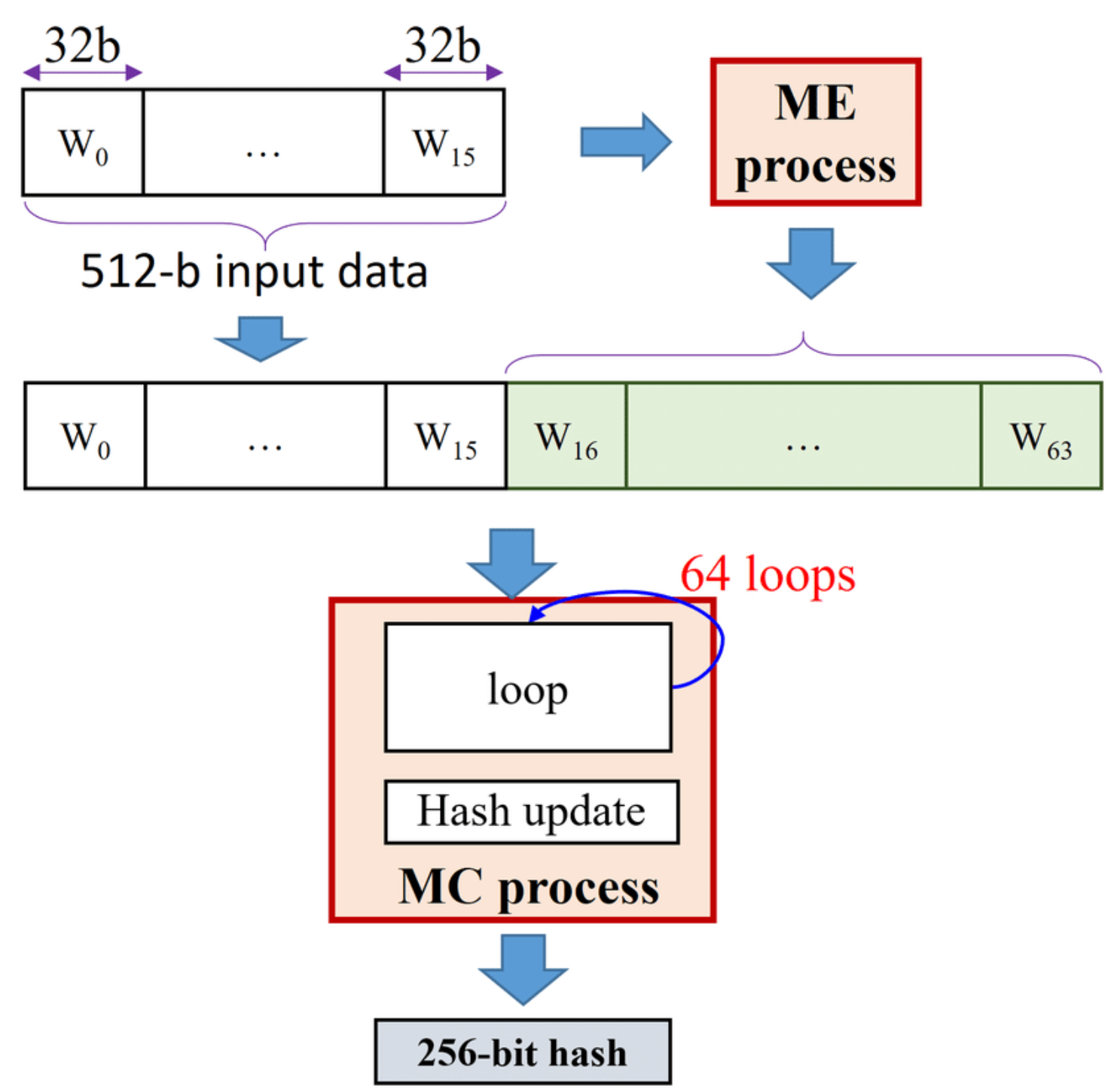
1)将第一个 512bit 的块数据分成 16 个字(512bit/32bit=16),记作 $W_{0}, W_{1}, …, W_{15}$
2)通过扩展函数ME process,将 16 个字(512bit)扩展为 64 个字
扩展函数为:$w_t = \sigma_1(w_{t-2}) + w_{t-7} + \sigma_0(w_{t-15}) + w_{t-16}$
其中:
$\sigma_0(x) = S^7(x) \oplus S^{18}(x) \oplus R^3(x)$
$\sigma_0(x) = S^{17}(x) \oplus S^{19}(x) \oplus R^{10}(x)$
$S^{n}$:循环右移 n 个 bit
$R^{n}$:右移 n 个 bit
3)接下来进行循环映射MC process,输入为上一步骤扩展得到的 64 个字$W_t$和初始化得到的$K_t$
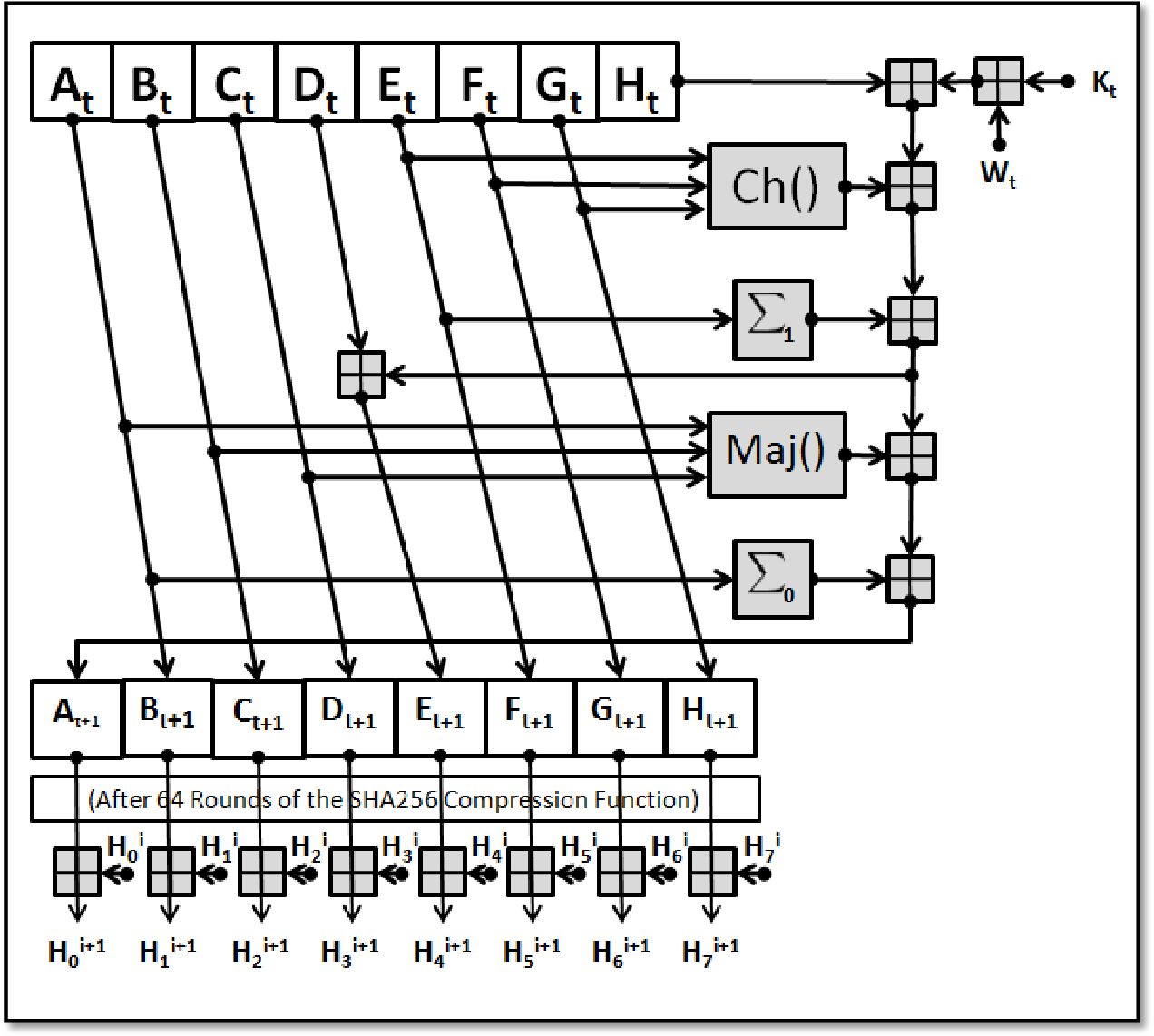
MC process的过程如上图所示,每一个块的运算需要迭代循环64次
其中涉及到四种新的运算:
-
$Ch(x, y, z) = (x \land y) \oplus (\neg x \land z) $
-
$Maj(x, y, z) = (x \land y) \oplus ( x \land z) \oplus ( y \land z) $
-
$\Sigma_0(x) = S^{2}(x) \oplus S^{13}(x) \oplus S^{22}(x) $
-
$\Sigma_1(x) = S^{6}(x) \oplus S^{11}(x) \oplus S^{25}(x) $
$A, B, C, D, E, F, G, H$ 8个字经过图中的运算得到循环更新,其中上述的4中新运算对其进行了非线性逻辑函数运算
而 $\boxplus$ 则表示相加后mod32,例如最右边的 $W_t \boxplus K_t$ 表示:
$ (W_t + K_t) \mod 32 $
这里需要注意的是:
- ABCDEFGH 一开始的初始值分别为 $H_{i-1}(0), H_{i-1}(1), …, H_{i-1}(7)$
- $K_t$ 是 64 个常量,每次循环使用 1 个常量。
- $W_t$ 是本区块产生第 t 个字(32bit),原消息被切成固定长度 512bit 的区块,对每一个区块,产生 64 个字,通过重复运行循环 n 次对 ABCDEFGH 这八个字循环加密
最后一次循环所产生的八个字合起来即得到哈希值
常见的计算SHA-256的方式
命令行工具(适用于大多数操作系统):
-
在 Linux 或 macOS 上,可以使用终端中的
sha256sum命令 -
在 Windows 上,可以使用 PowerShell 中的命令:
certutil -hashfile yourfilename SHA256
在线网站计算 SHA-256 哈希值:
https://emn178.github.io/online-tools/sha256_checksum.html
https://www.browserling.com/tools/sha256-hash
https://www.freeformatter.com/sha256-generator.html
代码实现
参见博主用Rust实现的SHA256哈希算法