Title: Three Horses
Creator: Xu Beihong
Date Created: 1919
Physical Dimensions: h 90, w 174 cm
Support: Paper
进入web3以来,越来越感受到密码学的重要性,尤其是开始研究zkp以后,更是如此。知识,亦是常学常新,在经过了zkp的洗礼之后,重新再来看基础密码学,也有颇多新解
本篇内容主要取材于Dr Lynndell的密码学讲座,不同于图解密码系列,而是更加深入的研究以太坊(Ethereum)使用的哈希函数 Keccak
核心原理
对称加密与哈希函数的核心原理:实现随机性
常见的实现方式主要包括三大变换:
-
线性变换:每 bit 的输入发生变换,影响 50%输出,密文随机性高
-
非线性变换: S-box (substitution-box),抵抗解方程组攻击、延展攻击
-
轮密钥加/轮常量加:添加一些随机密钥或常量,提高信息商
SHA3 Keccak
在以太坊(Ethereum)中,Keccak-256哈希函数主要用于以下几个方面:
地址生成:以太坊中,使用Keccak-256对公钥进行哈希计算,然后取哈希结果的后20个字节(160位),将其转换为以太坊地址格式
交易哈希:在以太坊中,使用Keccak-256对交易的原始数据(包括发送者地址、接收者地址、转移的以太币数量等)进行哈希计算,生成交易的哈希值
合约代码哈希:在以太坊部署智能合约时,会使用Keccak-256对合约的字节码进行哈希计算,生成一个唯一的合约代码哈希,这个哈希值用于唯一标识合约,并在以太坊网络中进行合约的部署和调用
Merkle树构建:以太坊中的状态树和交易树都是通过Merkle树结构来组织和验证数据
整体流程
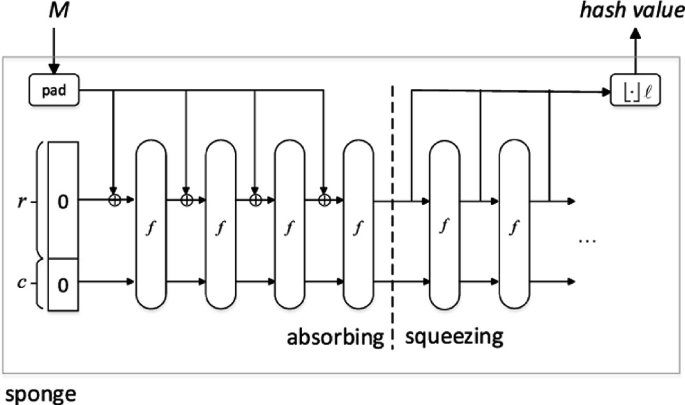
从图上可以看到,Keccak主要采用一种叫做海绵结构(Sponge construction)的结构进行处理,消息数据 $M$ 先进行数据填充的预处理,然后进行分片后进行吸入(absorbing)和挤出(squeezing)阶段,其中包含了Keccak最重要的轮函数,最后在挤出阶段根据设定的长度进行输出
海绵结构
海绵结构通常由两个参数定义: r,c
-
r表示比特速率(bit rate),决定了海绵结构的吞吐量,其值为每个输入块的长度 -
c表示容量(capacity),长度通常是输出长度的两倍。例如,对于Keccak-256哈希函数,输出长度为256bit,因此容量c为512bit -
b表示向量的长度,$b = r + c$,b的值依赖于指数L: $b=25*(2^L)$,对于Keccak-256哈希函数,一般取$L=6 ,b=1600$
r 和 c 常见的取值如下图:
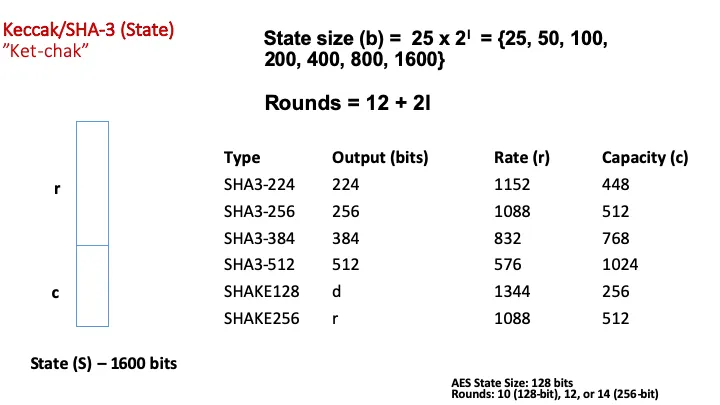
一般我们都是使用的SHA3-256,即取 r = 1088, c = 512
数据填充
在数据填充阶段,对输入串x做padding,使其长度能被 r = 1088 整除,将 padding 后分割成 长度为 r = 1088bits 的块
填充规则为 $msg’ = \lbrace msg, 1000…01 \rbrace$,即首尾填充1,中间补0
填充的长度要求满足: $(Len(msg) + 2 + k ) / r = 0 $,寻找最小自然数 k 即为中间 0 的长度
吸入阶段
此后在做轮函数计算时,每次对 (r + c)bit 的数据块进行运算,得到的 (r + c)bit 再与下一个块进行运算,如此运行 n 次则完成了吸入(absorbing)阶段
具体过程为:
1)首先初始化一个长度为 b=r+c bit的全零向量 $s$,记作 $S_0$
2)每一轮运算现将 $X_i$ 经过上述的填充后再与 $S_i$ 进行异或操作,结果记作 $S_{i}’$
3)$S_{i}’$ 经过轮函数之后作为下一轮的新状态 $S_{i+1}$,重复进行,直到将所有的填充块都用完
挤出阶段
1)在吸入阶段最后输出的状态 $s$,截取其长为 r 的块作为 $y_0$
2)将向量 $y_0$ 输入到 keccak-f 函数中处理,输出 $y_1$,以此类推,得到的 hash序列即为$y_0$、$y_1$、…、$y_i$
3)根据设定好的输出长度,当$y_{0…i}$ 的总长度大于设定的输出长度时,停止操作,根据输出长度取对应的前缀即可
所以Keccak是可以输出任意长的哈希值
轮函数
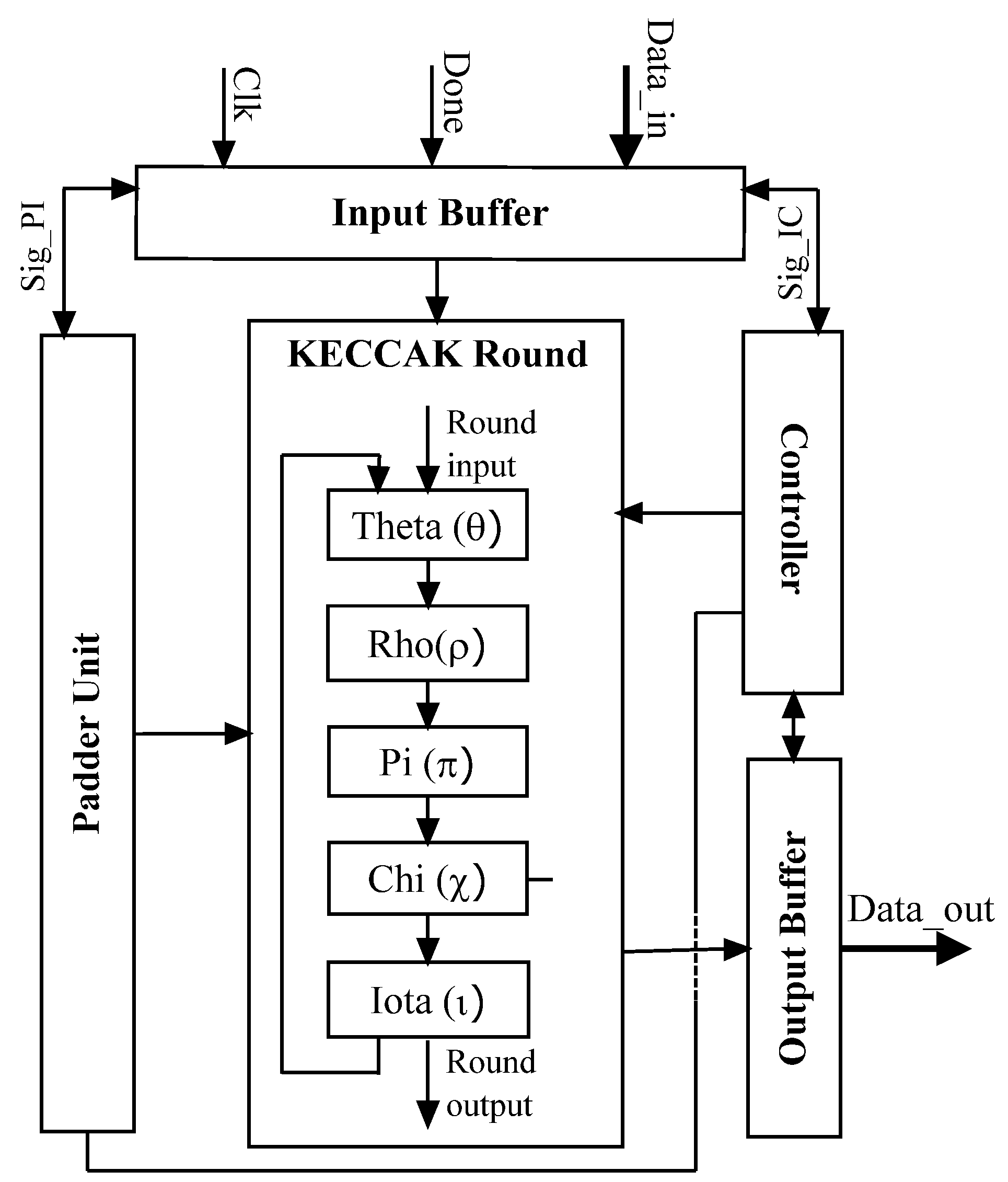
由上图可以看出,Keccak的轮函数主要包括了五个子函数:$Theta(\theta)$、$Rho(\rho)$、$Pi(\pi)$、$Chi(\chi)$、$Iota(\iota)$,这五个子函数中$Theta(\theta)$、$Rho(\rho)$、$Pi(\pi)$属于线性变换,$Chi(\chi)$属于非线性变换,$Iota(\iota)$属于轮常量加
一次轮函数的运算包括了$n_r$轮迭代,$n_r$的取值与之前计算 b 时用到的指数 L 成线性关系:
$
L = log_2 W = log_2 64 = 6 \\
n_r = 12 + 2L = 12 + 2 * 6 = 24
$
所以,当L取6时,$n_r$取值为24轮
AES中每轮计算将数据排成了二维平面(row、column)进行计算,不同于AES,Keccak在每轮计算中将b = 1600 bit的数据排列成了三维立体(row、column、lane):5 * 5 * 64
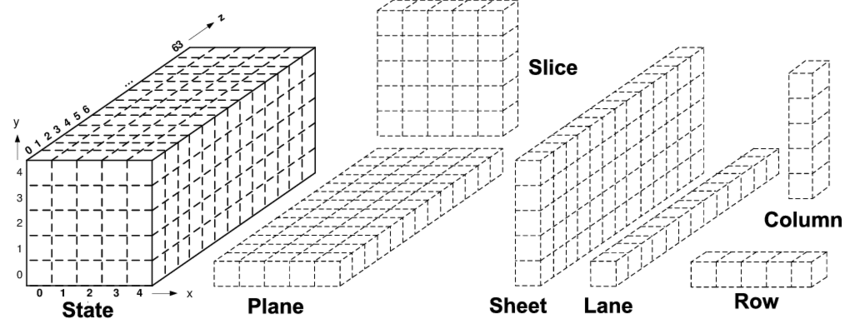
这里,我们设定row为 x轴,column为 y轴,lane为 z轴,所以任意一个 bit 可以表示为:$a[x][y][z]$
接下来我们详细介绍下五个子函数的计算过程
$Theta(\theta)$
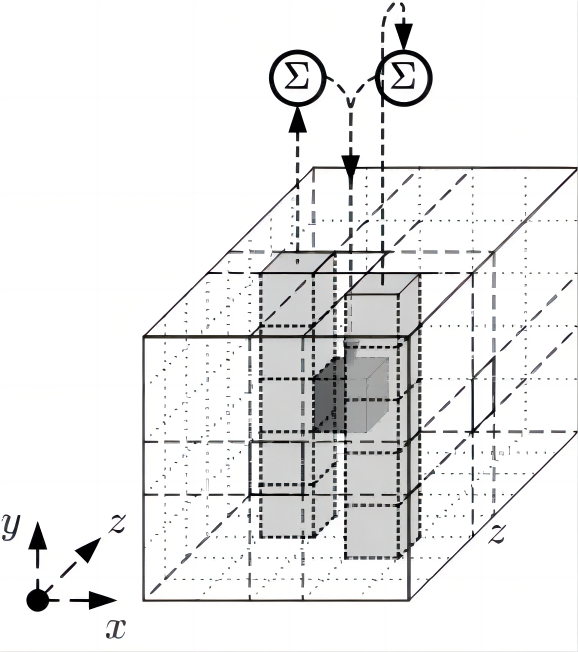
如上图所示,$Theta(\theta)$函数就是将该点与该点周围2列的元素之和再相加,其计算公式为:
$ a’[x][y][z] := a[x][y][z] + \sum_{y’=0}^{4}a[x-1][y’][z] + \sum_{y’=0}^{4}a[x+1][y’][z-1] $
图中的例子即为:
$ a’[3][3][4] := a[3][3][4] + \sum_{y’=0}^{4}a[2][y’][4] + \sum_{y’=0}^{4}a[4][y’][3] $
$Rho(\rho)$
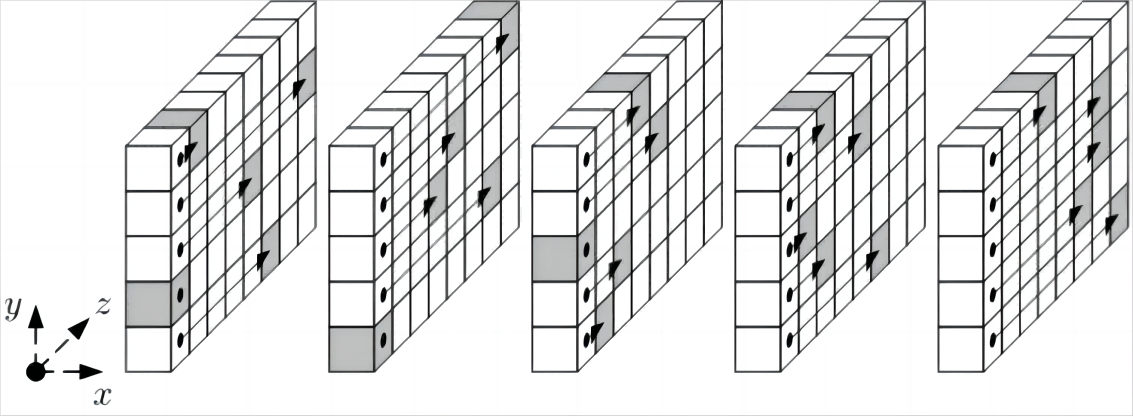
如上图所示,$Rho(\rho)$函数就是将点在深度方向(z轴)循环移位,其计算公式为:
$a’[x][y][z] := a[x][y][z - (t + 1)(t + 2)/ 2], t \in [0, …, 24], (x, y)=(1, 0)$ \(\begin{pmatrix} 0 & 2 \\ 1 & 3 \\ \end{pmatrix}^t\)
举个例子:
当$t=1$时,计算得到$(x, y) = (0, 2)$
此时:$a’[0][2][z] := a[0][2][z-3]$
$Pi(\pi)$
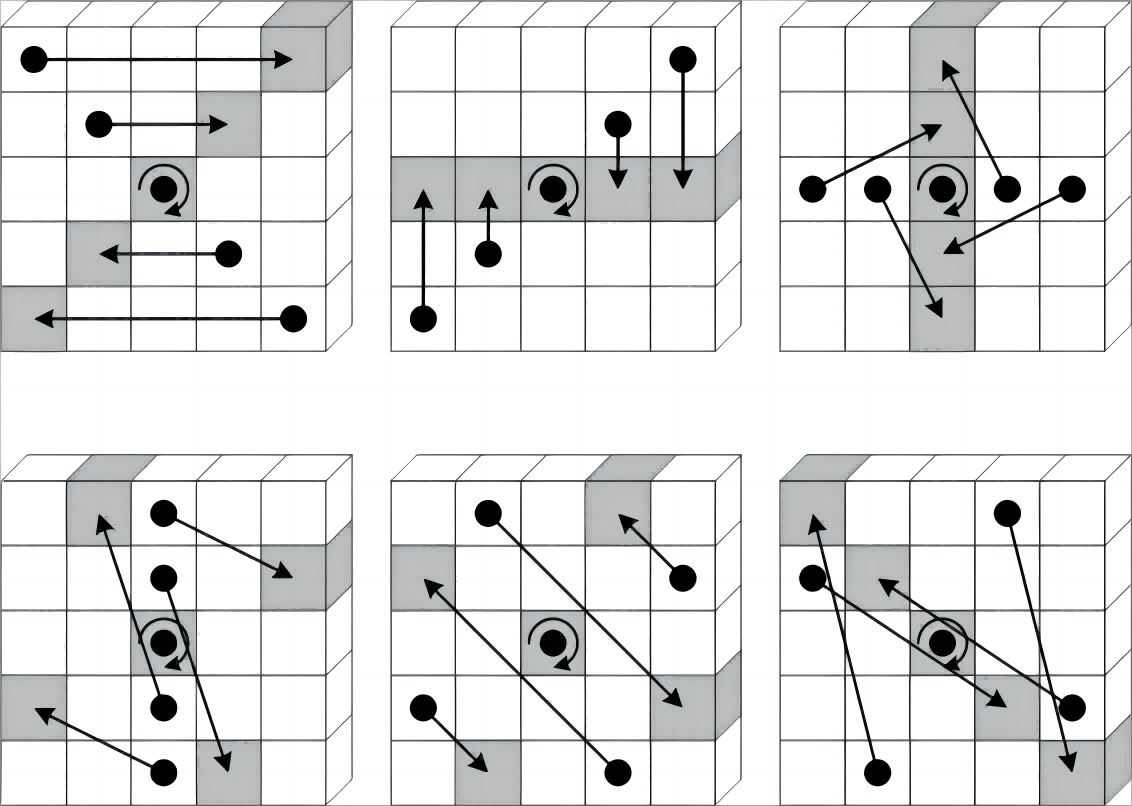
如上图所示,$Pi(\pi)$函数就是将点在平面(xy平面)进行旋转,其计算公式为:
$a[x’][y’] := a[x][y],$ \(\begin{pmatrix} x' \\ y' \\ \end{pmatrix}= \begin{pmatrix} 0 & 1 \\ 2 & 3 \\ \end{pmatrix}^t \begin{pmatrix} x \\ y \\ \end{pmatrix},\) $t=0, 1, …, 23$
$Chi(\chi)$
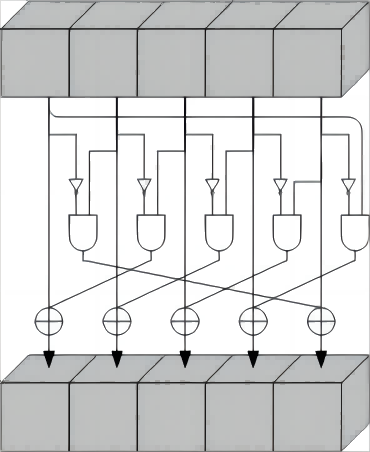
$Chi(\chi)$ 为Keccak中唯一的非线性变换,如上图所示,$Chi(\chi)$使用了三种逻辑运算实现了非线性变换,其公式为:
$For \quad x=0, …,4 \lbrace $
$For \quad y=0, …,4 \lbrace $
$a’[x][y]= a[x][y] \oplus (\neg a[x+1][y]) \wedge a[x+2][y]$
$\rbrace$
$\rbrace$
$Iota(\iota)$
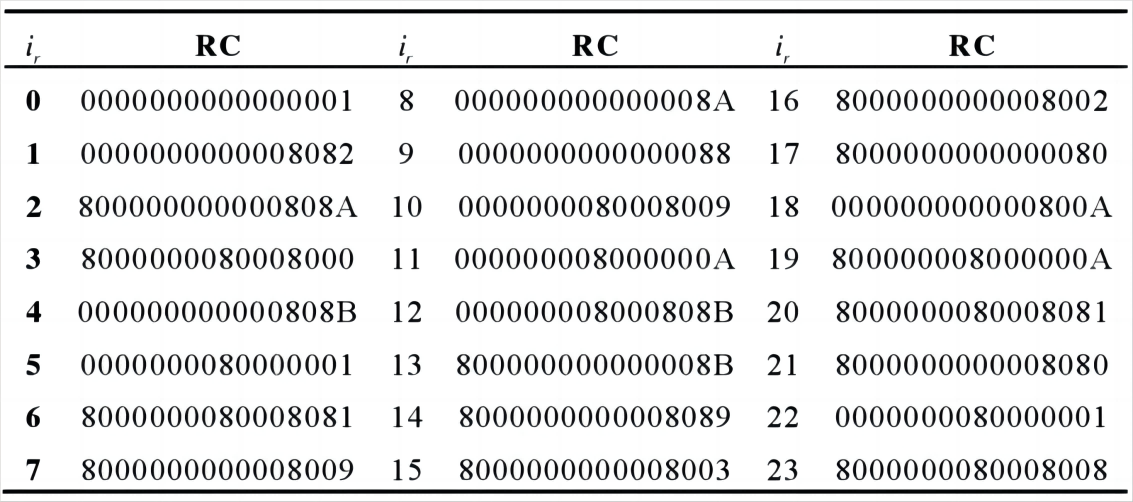
$Iota(\iota)$ 为Keccak中的轮常量加变换,它为keccak算法消除了对称性,其公式为:
$a’[0][0]= a[0][0] \oplus RC, z=0, 1, …, 23$
其中 RC 的值如下图所示:
伪代码
最后,我们使用伪代码来表示keccak中的轮函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Keccak-f[b](A) {
for i in 0…n-1
A = Round[b](A, RC[i])
return A
}
Round[b](A,RC) {
# θ step
C[x] = A[x,0] xor A[x,1] xor A[x,2] xor A[x,3] xor A[x,4], for x in 0…4
D[x] = C[x-1] xor rot(C[x+1],1), for x in 0…4
A[x,y] = A[x,y] xor D[x], for (x,y) in (0…4,0…4)
# ρ and π steps
B[y,2*x+3*y] = rot(A[x,y], r[x,y]), for (x,y) in (0…4,0…4)
# χ step
A[x,y] = B[x,y] xor ((not B[x+1,y]) and B[x+2,y]), for (x,y) in (0…4,0…4)
# ι step
A[0,0] = A[0,0] xor RC
return A
}