Title: Jiu Fanggao
Creator: Xu Beihong
Date Created: 1931
Physical Dimensions: h 139, w 351 cm
Support: Paper
进入web3以来,越来越感受到密码学的重要性,尤其是开始研究zkp以后,更是如此。知识,亦是常学常新,在经过了zkp的洗礼之后,重新再来看基础密码学,也有颇多新解
本篇内容主要取材于Dr Lynndell的密码学讲座,我们将深入的研究目前在zkp项目中经常使用的zk-friendly哈希函数——Poseidon
核心原理
对称加密与哈希函数的核心原理:实现随机性
常见的实现方式主要包括三大变换:
-
线性变换:每 bit 的输入发生变换,影响 50%输出,密文随机性高
-
非线性变换: S-box (substitution-box),抵抗解方程组攻击、延展攻击
-
轮密钥加/轮常量加:添加一些随机密钥或常量,提高信息商
ZK-friendly 哈希函数
我们上两篇文章 Web3中的哈希函数之SHA256 和 Web3中的哈希函数之Keccak 中研究的SHA256和SHA3-Keccak 这种标准化哈希函数已被广泛研究,安全性也得到了广泛的验证,它们的传统软件和硬件实现效率相对其他的哈希函数也更高
然而,许多 zk 协议使用的是相对陌生的哈希函数,而不是 SHA-2 和 SHA-3,造成这种情况的主要原因是,zk 协议的效率的确定方式与传统指标(例如运行时间、功耗和门数)完全不同 ,zk 协议中电路的效率取决于它们的代数结构
一般来说,如果电路在大范围内表示为简单表达式,则可以在证明者执行时间和证明大小方面进行有效证明,但传统的哈希函数并不适合于此
例如,当在 zk-STARK 中计算哈希时,SHA-2 的效率比 zk-friendly 的哈希函数低约 50-100 倍
ZKP(零知识证明)相关的内容后续会有更详细的系列博客讲解,在这篇文章中,我们先介绍 zk-friendly 哈希函数中的 Poseidon
Poseidon
Poseidon 的结构跟 Keccek 的结构一样,都是用了海绵结构(这里我们使用 $p$ 表示 Poseidon Hash 的轮函数)
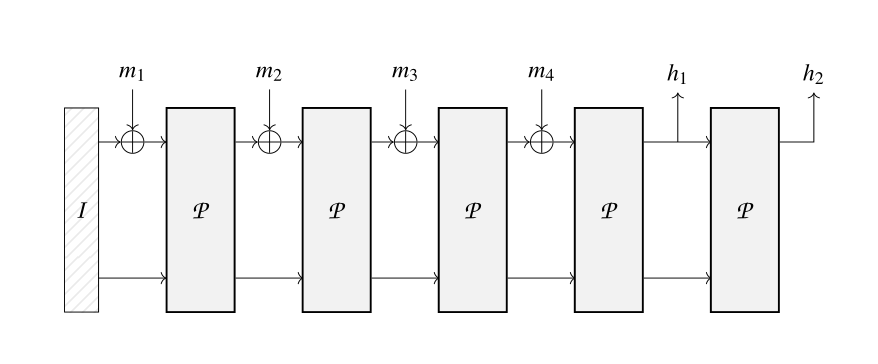
其整体结构和介绍可以详见上一篇博客中介绍的 海绵结构
这里我们主要介绍Poseidon哈希函数最重要也是不同于Keccak的地方——轮函数
轮函数
Poseidon 的轮函数主要有两种类型:Full rounds 和 Partial rounds,下图中标识为 $R_f$ 和 $R_p$
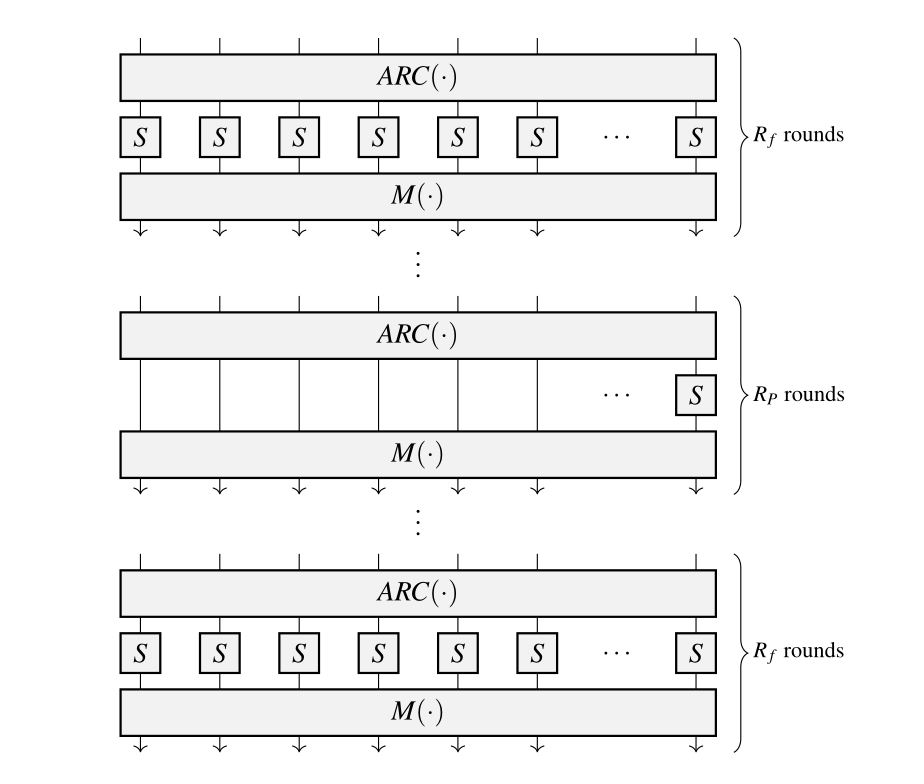
图中可以看到,初始初始时包含 $R_f$ 轮,此时状态会作用于所有的 S-box, 接着再进行 $R_p$ 轮,但是每轮仅包含一个 S-box,其余状态未作用 S-box 的状态通过一个非线性层(也即以一个恒等函数来代替缺失的 S-box),最后再进行一次 $R_f$ 轮的全 S-box
Poseidon 的每个轮函数由三个子函数组成:
1)$ARC(·)$(轮常量加)
轮常量与state进行相加
2)$S(·)$(非线性变换)
S-box主要有两种:
α 幂 - S-box:定义为 $S(x)=x^α$,其中 α 为满足 $gcd(α,p−1)=1$ 的最小正整数,对应的置换记为 $x^α − POSEIDON^π$ ,当 α=5 时,置换适用于 BLS12-381 和 BN254 两条曲线
逆 S-box:定义为 $S(x)=x^{−1}$ ,S(0)=0,对应的置换记为 $x^{−1} − POSEIDON^π$
一般在实际应用时,常用 $S(x) = x^5$
3)$M(·)$(线性变换)
这一层需要用到一个 $t * t$ 的满秩矩阵(Maximum Distance Separable matrix, MDS矩阵),其中 $2t + 1 \leq p$
三个组成部分以 $ARC -> S -> M$ 的方式一次执行,共执行 $R$ 轮,其中$ARC$和$M$每轮执行都相同,$S$如上所说,在第一次和最后一次相同,中间不同
应用
POSEIDON 可用于各类 ZKP 友好的 Hash 中,比如下面这几类
-
POSEIDON可用于协议中的承诺部分,效率比Pedersen承诺更高,且适用于签名
-
对多元素对象进行Hash
-
用POSEIDON Hash构建Merkle Tree
-
在集成加密方案(Intergrated Enc Scheme)中进行可验证加密
部分协议中已经采用了 POSEIDON Hash,比如 Filecoin 中用于构建 Merkel Tree 证明,Dusk Network 中用于构建类似于 Zcash 的安全交易协议等
结尾
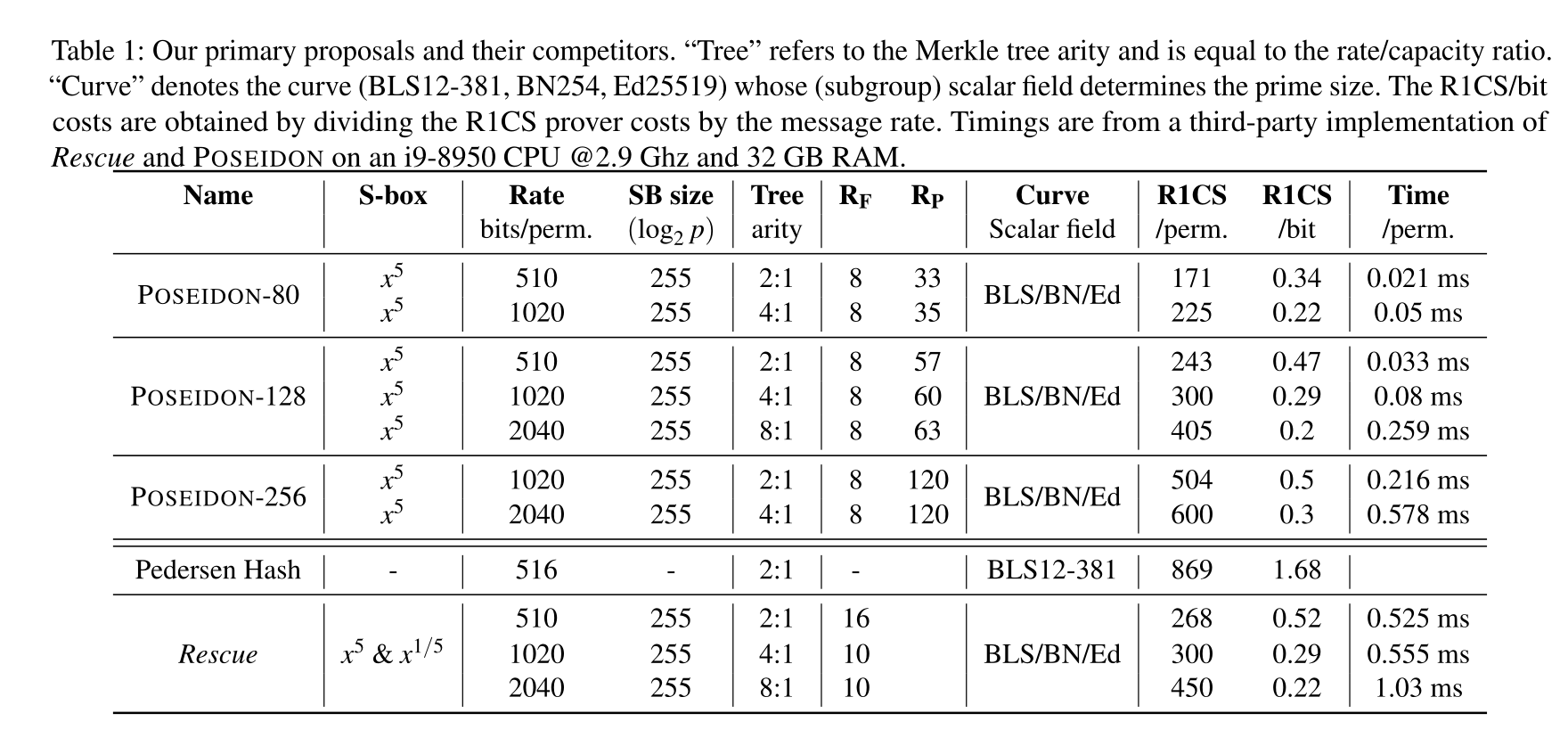
最后,贴一张表,表中记录了基于 R1CS 和 AET 的 POSEIDON 约束数量,其中 BLS 表示 BLS12-381 曲线,BN 表示 BN254 曲线,Ed 表示 Ristretto 群