Title: Running Together
Creator: Xu Beihong
Date Created: 1942
Physical Dimensions: h 95, w 181 cm
Support: Paper
进入web3以来,越来越感受到密码学的重要性,尤其是开始研究zkp以后,更是如此。知识,亦是常学常新,在经过了zkp的洗礼之后,重新再来看基础密码学,也有颇多新解
本篇内容主要取材于Dr Lynndell的密码学讲座,在现代密码学中,素数群和椭圆曲线群是两个常用的数学结构。素数群上的Diffie-Hellman和ElGamal算法以及椭圆曲线群上的ECDH和ElGamal算法,为密钥交换和公钥加密提供了强大的工具。本文将对素数群和椭圆曲线群进行比较,深入探讨它们在密码学中的应用,以及Diffie-Hellman和ElGamal算法在两种群上的实现方式
素数群与椭圆曲线群
群的概念
群(Group)是一种抽象的代数结构
抽象代数关注代数系统中的运算规则和结构,而不依赖于具体的数值或对象
抽象代数的核心概念包括群、环、域等代数结构:
- 群是一种集合与运算的组合,满足封闭性、结合律、单位元和逆元等性质
- 环是在加法和乘法下封闭的集合,并满足一些特定的性质,例如结合律、分配律等
- 域是一个满足一定性质的交换环,其中每个非零元素都有乘法逆元
这里我们先介绍群$G$的性质:
1)非空集:集合中至少有一个元素
2)二元运算:集合中的元素能够进行一种运算,例如加法运算或乘法运算
3)封闭性:集合中的元素进行运算后,得到的结果仍然是集合中的元素
4)结合律:任意 $a,b,c$ 属于群 $G$,则 $(a+b)+c=a+(b+c)$
5)单位元 $e$:加法情况下 $a+e=e+a=a$;乘法情况下: $a*e=e*a=a$
6)每个元素 $a$ 都有逆元,记为 $a^{-1}$: 加法情况下:$a + a^{-1}= a^{-1}+a=e $;乘法情况下:$a * a^{-1} = a^{-1} * a = e$
举个例子:
整数集合 $\mathbb{Z}$ 和加法运算
1)整数相加的结果还是整数,满足封闭性
2)整数加法满足结合律
3)单位元是0,任何整数加0都等于这个整数本身
4)整数的逆元素就是它的相反数,比如 $2$ 的逆元是 $-2$
因此整数集合 $\mathbb{Z}$ 和加法运算具有群的性质,它们构成了整数加法群,记作 $(\mathbb{Z}, +)$
再来一个:
模 $n$ 的单元集(Unit set) $\mathbb{Z}_n^*$ 和乘法运算
1)模 $n$ 的单元集 $\mathbb{Z}_n^*$ 的乘法封闭
2)模运算中的乘法满足结合律
3)单位元是1,任何单位乘以1都等于这个它本身
4)模 $n$ 的单元集中的元素都有逆元,两者乘积为 $1$
因此模 $n$ 的单元集 $\mathbb{Z}_n^{*}$ 和乘法运算满足群的性质,它经常被称为整数模n乘法群,记作 $(\mathbb{Z}_n^{*}, \times)$
上面两个例子中, $(\mathbb{Z}, +)$ 群中的个数是无限的,所以称为无限群(Infinite Group);而 $(\mathbb{Z}_n^{*}, \times)$是有限的,所以称为有限群(Finite Group)
另外两个重要概念:
生成元:如果一个群元素 g 能够通过有限次自身运算,表达群内其他所有元素,则称为群的 生成元
阶:群内元素个数称为群的阶
单位元是唯一的,生成元可以有多个
椭圆曲线群
椭圆曲线不是我们日常所理解的椭圆形状,而是满足特定方程的点的集合。这个方程通常被写为: $y^2 = x^3 + ax + b, 4a^3 + 27b^2 ≠ 0$
这里直观的看看椭圆曲线的形状,它是无奇点的,即没有尖点,且不会自相交
当 a,b 的值不同时,椭圆曲线会表现出不同的形态:
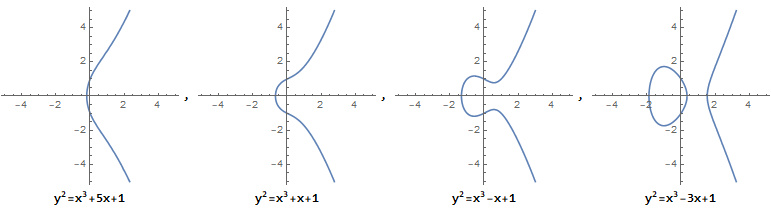
从图中可以看到,椭圆曲线总是沿 x 轴对称的。这是因为 $y^2$ 的存在。特殊地,我们规定无穷远点也存在于椭圆曲线上,记作 $O$
椭圆曲线上的点运算
椭圆曲线上的点运算主要是点加和点乘,其中点加的几种情况如下图所示:
加法
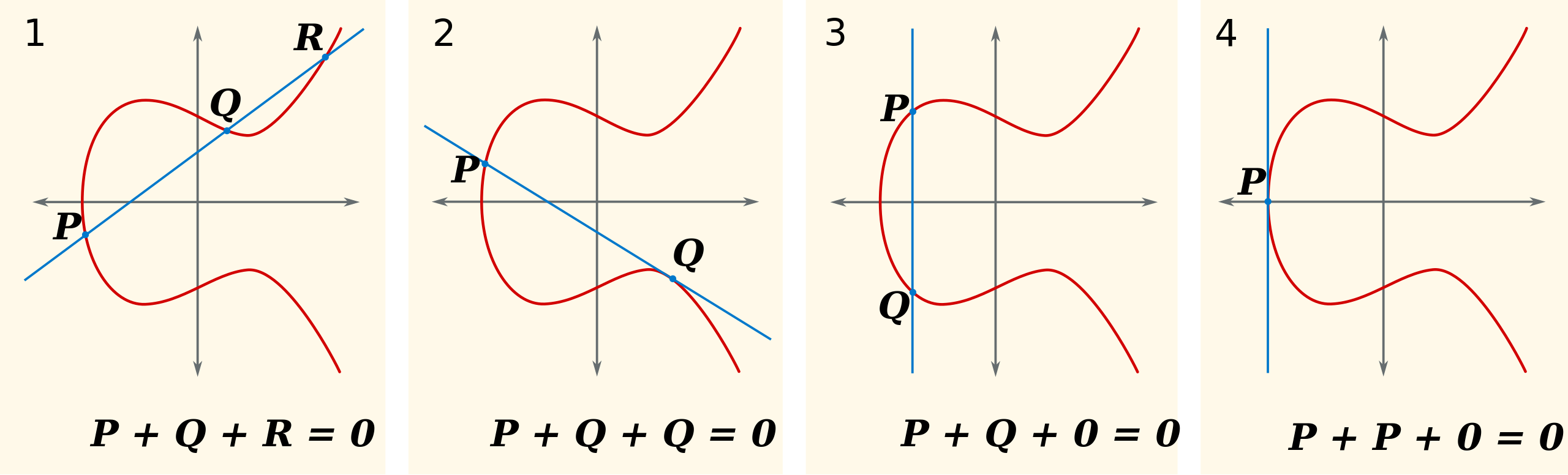
1)如果 $P≠Q$,且 $x_p≠x_q$ ,则过 $P,Q$ 的直线会与椭圆曲线相交于第三点,记作 $R$, 同时定义取椭圆曲线上沿 x 轴对称的点的操作为 $-$ ,则可知$R$沿x轴的对称点为$-R$, 因此可得 $P+Q=-R,P+Q+R=0$
2)在1的基础上,如果$P,Q$的直线刚好与椭圆曲线相切于$Q$点,则此时可理解为$R$点与$Q$点重合,所以得$P+Q=-Q,P+Q+Q=0$
此时也可以理解为,$2Q$的计算方式:在曲线上对$Q$做切线,与曲线相交的点的对称点即为$2Q$
3)如果 $P≠Q$ ,且 $y_p=−y_q$ (即 $P,Q$ 沿 x 轴对称,过 $P,Q$ 的直线垂直于 x 轴), 则此时 $P+Q=0$
4)如果 $P=Q$,且在x轴上,则可以明显得到 $P+P+0=0$
加法运算定义了椭圆曲线上的以 0 为单位元的群
乘法
定义椭圆曲线上的标量乘法:若 $P$ 是椭圆曲线上的点,n 是正整数,则 $nP = P + P +…+ P$
下面我们来实际计算下点乘:
假设 $n=88$
1)方法1: \(2P = P + P \\\ 3P = 2P + P \\\ ... \\\ 88P = 87P + P\)
总共需要计算 88 - 1 = 87次
2)方法2: \(2P = P + P \\\ 4P = 2P + 2P \\\ 8P = 8P + 8P \\\ 16P = 8P + 8P \\\ 32P = 16P + 16P \\\ 64P = 32P + 32P \\\ 88P = 64P + 16P + 8P\)
总共需要计算 7 次,明显效率要高很多
因此,我们可以设定,现将n用二进制表示,即:
$ n = n_0 + 2n_1 + 2^2n_2 + 2^3n_3+ 2^4n_4 + … + 2^mn_m, 其中s_0,s_1…s_m \in {0, 1}, m=log_2s$
计算 $nP$ :
$ nP = n_0P + 2n_1P + 2^2n_2P + 2^3n_3P + 2^4n_4P + … + 2^mn_mP, 其中s_0,s_1…s_m \in {0, 1}, m=log_2s$
该方法中求 $2^xP$ 的时间复杂度为$O(1)$, 所以整个的 时间复杂度为 $O(log_2n)$
有限域上的椭圆曲线
在实际的web3应用中,我们一般使用的是有限域上的椭圆曲线,所以这里简单介绍下什么是有限域上的椭圆曲线群
椭圆曲线在素数 $p$ 的有限域 $F_p$ 上的点的集合为:
$y^2 \equiv x^3 + ax + b (\mod p), 4a^3 + 27b^2 \neq 0(\mod p)$
所有的值都在有限域 $F_p$ 上
此时椭圆曲线描述的不再是上述平滑的曲线,而是离散点的集合(这些点关于 $y = P/2$ 对称)
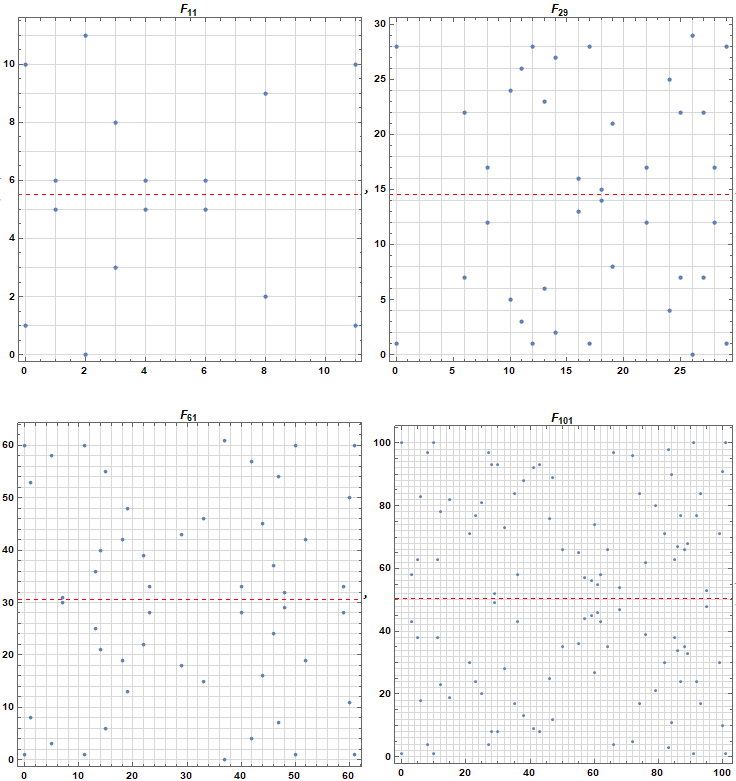
此外,椭圆曲线群除了具备素数群的性质外,还多一个交换律的性质(阿贝尔群)
有限域上的点运算
前面我们定义了实数域上椭圆曲线两个点进行点加和点乘运算的几何和代数意义,这个意义在有限域内依然是成立的,只是多了 $( \mod p )$ 的模运算
此外,直线也需要进行$( \mod p )$运算
下面的例子,展示了当 $p=29$ 时,点 $P(0,1),Q(1,7)$ 在椭圆曲线 $y^2≡x^3+x+1(\mod p)$ 上,此时 $R=P+Q$ 如下所示:
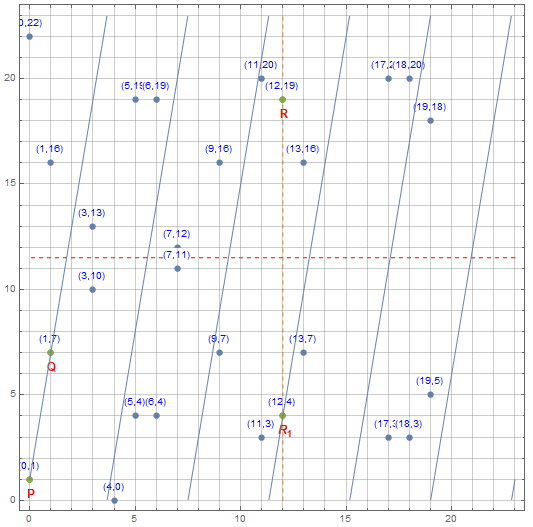
可以看到,当 $y$ 超出范围后,又从0开始,表示模运算;而在第三次从0开始的连线上,终于与群内的离散点相交,此时交点即为$-R$(图内为$R_1$),其对称点即为 $R$
离散对数问题
离散对数
如果对于一个整数 $b$ ,和素数 $p$ 的一个原根 $g$ ,可以找到一个唯一的指数 $x$ ,使得:
$b \equiv g^x (\mod p)$,其中 $ 0 \leq x \leq p-1$
那么 $x$ 就为 $b$ 的以 $g$ 为基数的模 $p$ 的离散对数
离散对数难题
素数群上的离散对数问题(DLP)
离散对数问题(Discrete Logarithm Problem, DLP)扩展到群上,就是对于群 $\mathbb{Z}_p^*$ ,其中 $p$ 为素数,给定生成元 $g$ 和元素 $b$,找到离散对数 $x$ 使得 $b\equiv g^x ( \mod p), 0 \leq x \leq p-1 $ 成立,这个问题在计算上是困难的,因为目前没有已知的高效算法可以在多项式时间内解决它
椭圆曲线群上的离散对数问题(ECDLP)
ECDLP的定义是:对于有限域上的椭圆曲线群 $\mathbb{E}$,给定曲线上的点 $P, Q$,找到 $Q=nP$ 成立的离散对数 $n=log_PQ$,这个问题在计算上是困难的,因为目前没有已知的高效算法可以在多项式时间内解决它
这里解释一下,已知 $P$ 和 $n$,求 $Q=nP$ 是容易的,思路就是与椭圆曲线相切于第三点,然后找对称点(也就是需要多做几次切线和少量的点加计算)
但是反之则属于困难问题,因为正向计算找切线,每次计算最多一个切点;但是反向计算,已知$P’$,如下图,如果是前文中的第二种情况,则会切出两个点,即图中的 $Q1 和 Q2$;当然也有一种情况是只有一个切点
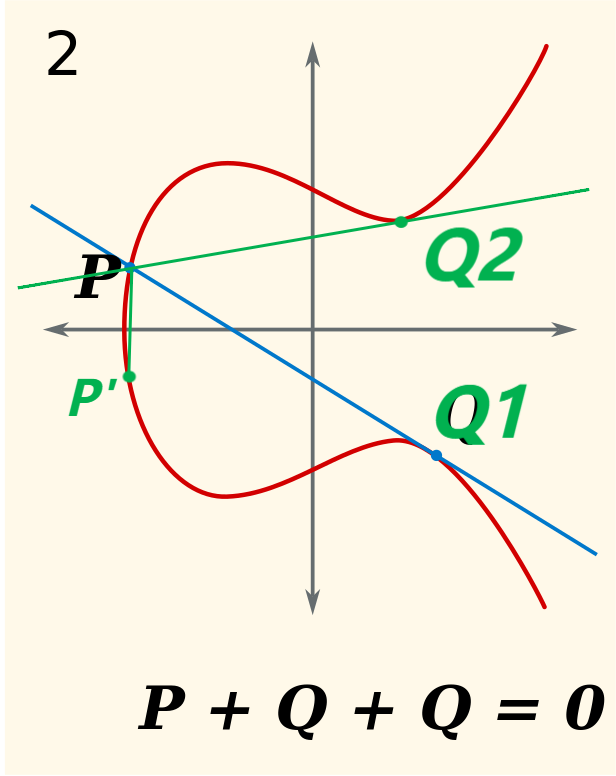
所以,第一次反向切,会出现1 or 2个点,第二次则是2 or 4个点,以此类推,计算复杂度和空间都呈指数增加
当$n=2^{256}$时,需要找 $n=2^{256}$个点,每次都要检测是否是$P$点,如果找到了就停止,没有则继续切继续找
注意:不是每条椭圆曲线的离散对数问题都是难解的,实际应用时应该使用经过实战检验的椭圆曲线
比特币主要使用的是 secp256k1 曲线
以太坊主要使用到了 secp256k1,alt_bn128,和 bls12_381 三条曲线
Diffie-Hellman
Diffie-Hellman 迪菲-赫尔曼密钥交换算法是由 Whitfield Diffie 和 Martin Hellman 在 1976 年首次提出的,它是一种公钥密码学算法,允许两个远程用户在不共享密钥的情况下达成一个共同的密钥
素数群上的 DH
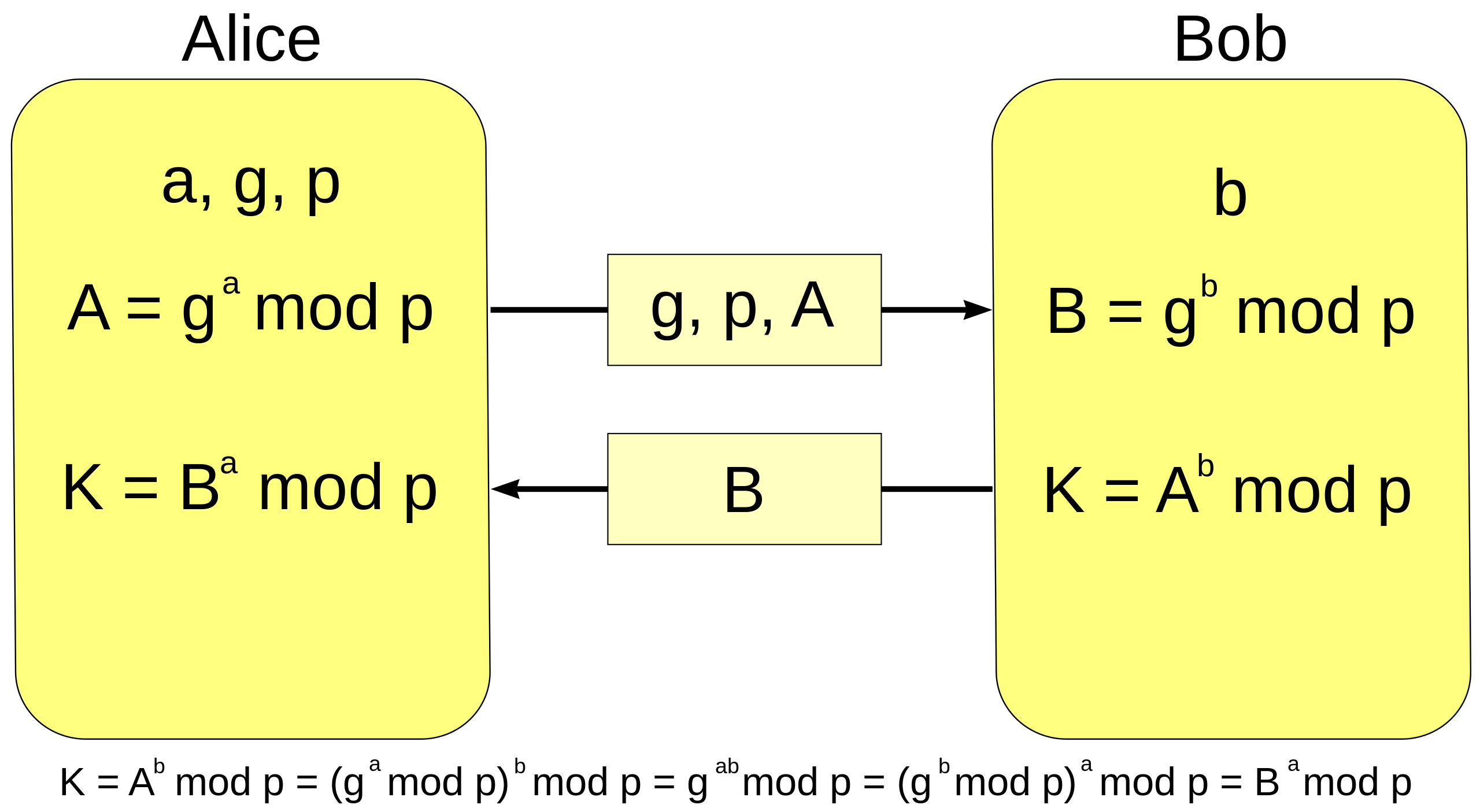
上图已经完整的诠释了其过程,其中 $p$ 为阶,$g$ 为生成元,$a$ 为 Alice的私钥,$A$ 为 Alice的公钥,$b$ 为 Bob的私钥,$B$ 为 Bob的公钥,$K$ 为 Alice 和 Bob 的共享密钥
DH 的安全依赖于离散对数难题,在选择了合适的G和g时,这个协议被认为是窃听安全的
椭圆曲线群上的DH(ECDH)
同理,在有限域的椭圆曲线上选择一个基点$G$,$a$ 为 Alice的私钥,$b$ 为 Bob的私钥,则:
Alice的公钥 $A = a·G$
Bob的公钥 $B = b·G$
交换公钥后,各自计算得到共享密钥 $K = a·B = ab·G = ba·G = b·A$
ECDH 的安全依赖于椭圆曲线上的离散对数难题
这里再介绍两个概念:
计算性DH难题(CDH):已知基点$G$,$a·G$,$b·G$,求 $ab·G$ 是困难的
判决性DH难题(DDH):已知基点$G$,$a·G$,$b·G$,$Z$,求 $Z$ 是否等于 $ab·G$ 是困难的
素数群上同理
DLP,CDH,DDH 是标准困难问题,是最安全的困难问题
ElGammal 公钥加密算法
ElGamal加密算法是一个基于Diffie-Hellman密钥交换的非对称加密算法,它在1985年由塔希尔·盖莫尔提出
素数群上的 ElGammal
ElGamal加密算法由三部分组成:密钥生成、加密和解密
素数群 $\mathbb{G}$ 的阶为 $p$,生成元为 $g$
密钥生成
1)Alice 选择一个随机数 $x, x \in \mathbb{Z}_p $ 作为私钥
2)计算 $H = g^x$,作为其公钥
加密
1)Bob 将消息编码为群元素 $m, m \in \mathbb{G}$,
2)选择一个随机数 $r, r \in \mathbb{Z}_p$ (保密)
3)计算密文 $C_1 = g^r, C_2 = H^r·m$
解密
Alice 收到 $( C_1, C_2)$密文后,使用私钥$x$进行解密:
$m = C_2·C_1^{-x}$
推导证明:
\(m = C_2·C_1^{-x} \\\
= H^r · m · (g^r)^{-x} \\\
= (g^x)^r ·m· (g^r)^{-x} \\\
= m\)
安全性:基于 DDH 困难问题
椭圆曲线群上的 ElGammal
椭圆曲线群 $\mathbb{G}$ 的阶为 $p$,基点为 $G$
密钥生成
1)Alice 选择一个随机数 $x, x \in \mathbb{Z}_p $ 作为私钥
2)计算 $H = x·G$,作为其公钥
加密
1)Bob 将消息编码到椭圆曲线群上, $M, M \in \mathbb{G}$,
2)选择一个随机数 $r, r \in \mathbb{Z}_p$ (保密)
3)计算密文 $C_1 = r·G, C_2 = M + r·H$
解密
Alice 收到 $( C_1, C_2)$密文后,使用私钥$x$进行解密:
$M = C_2 - x·C_1$
推导证明:
\(M = C_2 - x·C_1 \\\
= M + r·H -x·C_1 \\\
= M + rx·G - xr·G \\\
= M\)
安全性:基于 DDH 困难问题
Hashed ElGammal 加密算法
在标准的 ElGammal 算法中,Bob 在加密时,需要先将消息m编码到素数群或者椭圆曲线群上,这会导致实际应用不方便,因此产生了Hashed ElGammal 加密算法,用来解决这个问题,这里我们主要介绍素数群上的Hashed ElGammal 算法,椭圆曲线上同理
素数群 $\mathbb{G}$ 的阶为 $p$,生成元为 $g$
密钥生成
1)Alice 选择一个随机数 $x, x \in \mathbb{Z}_p $ 作为私钥
2)计算 $H = g^x$,作为其公钥
加密
1)Bob 将消息拆分,$m, m \in \lbrace 0,1 \rbrace ^{256}$,
2)选择一个随机数 $r, r \in \mathbb{Z}_p$ (保密)
3)计算密文 $C_1 = g^r, C_2 = hash(H^r) \oplus m$
解密
Alice 收到 $( C_1, C_2)$密文后,使用私钥$x$进行解密:
$m = C_2 \oplus hash(C_1^{x})$
推导证明:
\(m = C_2 \oplus hash(C_1^{x}) \\\
= hash(H^r) \oplus m \oplus hash(g^{rx}) \\\
= hash(g^{xr}) \oplus m \oplus hash(g^{xr}) \\\
= m\)
安全性:基于 CDH 困难问题,但是由于引入了hash函数,所以有归约损失$q_{hash}$,通常是$2^{40}$
即如果密钥长度为256bit,则算法安全性为216bit